/Szkoła średnia

Równania i nierówności wymierne

Równania wymierne Równanie wymierne to równanie, które można sprowadzić do postaci

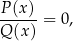
P-(x)- Q (x) = 0 ,

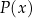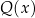gdzie P(x) i Q (x) to pewne wielomiany.

Oczywiście każde rozwiązanie powyższego równania musi spełniać równanie wielomianowe 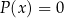P(x ) = 0 (licznik musi być równy 0). Z tego punktu widzenia rozwiązywanie równań wymiernych sprowadza się do rozwiązywania równań wielomianowych.

Rozwiążmy równanie 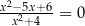x2−-5x+6- x2+4 = 0 .
Od razu zajmujemy się licznikiem. Liczymy.

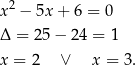
x2 − 5x+ 6 = 0 Δ = 25 − 2 4 = 1 x = 2 ∨ x = 3.

Jest jednak jeden drobny, aczkolwiek bardzo istotny szczegół, liczba 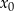x0 dla której 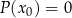P(x0) = 0 może być jednocześnie zerem mianownika wyrażenia 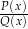P(x) Q(x) . W takiej sytuacji nie jest to rozwiązanie wyjściowego równania (nie należy do jego dziedziny).

Łatwo sprawdzić, że liczba 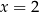x = 2 jest miejscem zerowym licznika ułamka 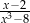x− 2 x3−8 , ale nie jest to rozwiązanie równania

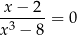
x-−-2--= 0 x3 − 8

bo dla 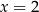x = 2 mianownik tego wyrażenia się zeruje.

Są dwa sposoby poradzenia sobie z problemem dziedziny równania wymiernego.
1. Pierwszy sposób to wyznaczenie na początku dziedziny równania. Musimy więc rozwiązać równanie wielomianowe 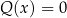Q (x) = 0 i jego pierwiastki wyrzucić z dziedziny równania. Przy takim podejściu rozwiązanie równania wymiernego 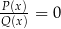P(x) Q(x) = 0 wymaga rozwiązania dwóch równań wielomianowych: 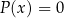P(x ) = 0 oraz Q(x ) = 0 .

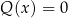Rozwiążmy równanie 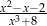x2−x-−2 x3+ 8 .
Mianownik zeruje się tylko dla 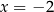x = − 2 , więc dziedziną równania jest zbiór 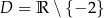D = R ∖{ −2 } . Szukamy teraz miejsc zerowych licznika.

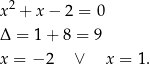
2 x + x− 2 = 0 Δ = 1 + 8 = 9 x = − 2 ∨ x = 1.

Pierwszy z pierwiastków nie należy do dziedziny równania.

2. Drugi sposób, który jest niezwykle wygodny w przypadku bardziej skomplikowanych mianowników, to sprawdzenie na koniec, czy otrzymane miejsca zerowe licznika nie są przypadkiem miejscami zerowymi mianownika. Przy takim podejściu nie musimy wyznaczać dziedziny równania.

Rozwiążmy równanie 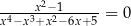x2− 1 x4−x-3+x-2−6x+5-= 0 .
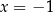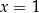W tym przykładzie wyznaczenie dziedziny równania byłoby niezwykle trudne, podczas gdy samo rozwiązanie równania jest bardzo proste: miejsca zerowe licznika to x = − 1 i x = 1 . Skoro jednak nie wyznaczyliśmy dziedziny, musimy sprawdzić, czy przypadkiem któraś z tych liczb nie jest miejscem zerowym mianownika. Liczymy

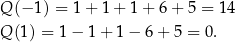
Q (− 1) = 1+ 1+ 1+ 6+ 5 = 14 Q (1) = 1− 1+ 1− 6+ 5 = 0.

Zatem jedynym rozwiązaniem równania jest 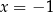x = − 1 .

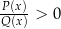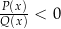Nierówności wymierne Sytuacja nierówności wymiernych jest odrobinę bardziej skomplikowana, bo tym razem musimy traktować znacznie poważniej mianownik ułamka (w przypadku równań w zasadzie nie miał on znaczenia, byle tylko był niezerowy). Rozpocznijmy od przypadku ostrej nierówności postaci P (x) Q-(x) > 0 lub P(x) Q-(x) < 0 . Sytuacja jest bardzo prosta, korzystając z równoważności

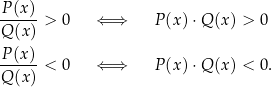
-P(x)-> 0 ⇐ ⇒ P(x) ⋅Q (x) > 0 Q (x) P(x) ------< 0 ⇐ ⇒ P(x) ⋅Q (x) < 0. Q (x)

zamieniamy taką nierówność na nierówność wielomianową.

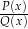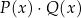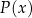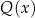Wyjaśnijmy krótko sens tych równoważności. Kiedy ułamek P(x) Q(x) jest dodatni? – dokładnie wtedy, gdy licznik i mianownik są tego samego znaku (oba dodatnie lub oba ujemne). A kiedy iloczyn P(x )⋅Q (x) jest dodatni? – gdy się chwilę zastanowimy to dokładnie w takiej samej sytuacji: gdy liczby P (x) i Q (x) są tego samego znaku. Innymi słowy

Iloraz dwóch liczb ma taki sam znak jak ich iloczyn.

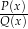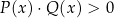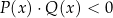Zauważmy jeszcze dodatkową miłą cechę tych równoważności: nie musimy w ogóle przejmować się dziedziną wyjściowego wyrażenia P(x) Q(x) . Dlaczego? Ano dlatego, że wśród rozwiązań nierówności P(x) ⋅Q (x) > 0 (lub P (x)⋅ Q(x ) < 0 ) nie może być liczb dla których 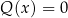Q (x) = 0 (bo wtedy 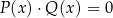P (x)⋅ Q(x ) = 0 ), czyli wszystkie rozwiązania, które otrzymamy są poprawne.

Zbiór rozwiązań nierówności 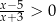xx−+53-> 0 jest taki sam jak zbiór rozwiązań nierówności kwadratowej

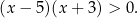
(x − 5 )(x + 3) > 0.

Jest to więc zbiór 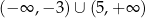(− ∞ ,− 3) ∪ (5,+ ∞ ) .

Rozwiążmy nierówność 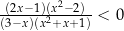(2x− 1)(x2−2) (3−x)(x2+x-+1) < 0 .
Dana nierówność jest równoważna nierówności

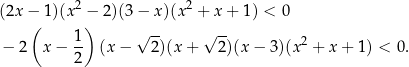
(2x − 1)(x2 − 2)(3 − x)(x 2 + x + 1 ) < 0 ( ) 1- √ -- √ -- 2 − 2 x− 2 (x− 2)(x+ 2)(x − 3)(x + x + 1) < 0 .

Ostatni czynnik jest zawsze dodatni, więc pozostaje nierówność

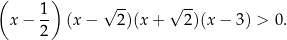
( 1) √ -- √ -- x− -- (x − 2)(x+ 2)(x − 3) > 0. 2
ZINFO-FIGURE

Korzystając teraz z metody węża mamy

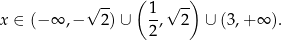
√ -- ( √ --) x ∈ (− ∞ ,− 2 )∪ 1, 2 ∪ (3,+ ∞ ). 2

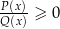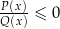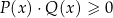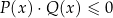Słabe nierówności Pozostał nam przypadek słabych nierówności postaci P(x) Q(x) ≥ 0 oraz P(x) Q (x) ≤ 0 . Sytuacja jest podobna jak w przypadku ostrych nierówności: zamieniamy te nierówności na nierówności P (x)⋅ Q (x ) ≥ 0 oraz P(x) ⋅Q (x) ≤ 0 odpowiednio. Tym razem jest jednak mały haczyk: w otrzymanym zbiorze rozwiązań będą zawarte zera mianownika 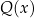Q(x ) (bo nierówność jest słaba) i musimy te zera usunąć. Innymi słowy, w tym przypadku nie możemy zignorować dziedziny nierówności. W skrócie zapisujemy tę sytuację przy pomocy równoważności

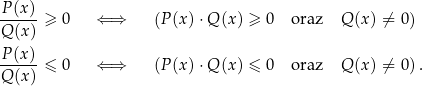
P (x) ------≥ 0 ⇐ ⇒ (P (x)⋅Q (x ) ≥ 0 oraz Q (x) ⁄= 0) Q (x) P-(x)- Q (x) ≤ 0 ⇐ ⇒ (P (x)⋅Q (x ) ≤ 0 oraz Q (x) ⁄= 0) .

Rozwiążmy nierówność 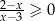2−x- ≥ 0 x− 3 .
Zamieniamy iloraz na iloczyn

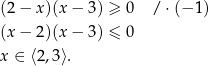
(2 − x )(x− 3) ≥ 0 / ⋅(− 1) (x − 2)(x− 3) ≤ 0 x ∈ ⟨2,3⟩.

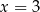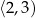Z otrzymanego przedziału musimy jednak wyrzucić zero mianownika, czyli x = 3 . Odpowiedzią jest więc przedział ⟨2 ,3 ) .

Powyżej wyświetlona jest tylko pierwsza część poradnika. Druga część jest dostępna tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.