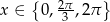/Szkoła średnia

Zadanie nr 3199473

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 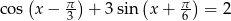( π-) ( π) cos x − 3 + 3sin x + 6 = 2 w przedziale ⟨0,2π ⟩ .

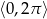Rozwiązanie

Sposób I

Zauważmy, że

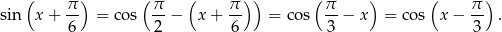
( π-) ( π- ( π-)) ( π- ) ( π-) sin x + 6 = co s 2 − x+ 6 = cos 3 − x = cos x− 3 .

Dane równanie możemy więc zapisać w postaci

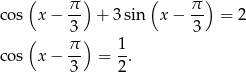
( π ) ( π ) co s x − -- + 3sin x − -- = 2 ( 3 ) 3 co s x − π- = 1-. 3 2

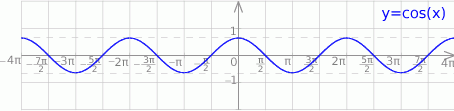
Szkicujemy cosinusa.

PIC

Mamy zatem

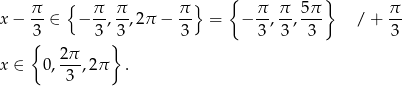
{ } { } x − π-∈ − π-, π-,2π − π- = − π, π-, 5π / + π- 3 3 3 3 3 3 3 3 { } x ∈ 0 , 2π-,2π . 3

Sposób II

Korzystamy ze wzorów na sinus/cosinus sumy/różnicy.

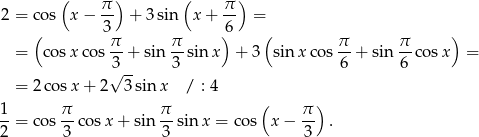
( π-) ( π-) 2 = cos x − 3 + 3 sin x+ 6 = ( π π ) ( π π ) = co sx cos-- + sin --sinx + 3 sin x cos-- + sin --cos x = √3-- 3 6 6 = 2co sx + 2 3 sin x / : 4 1 π π ( π) --= cos --cos x+ sin --sin x = co s x − -- . 2 3 3 3

Dalej równanie rozwiązujemy tak samo jak w pierwszym sposobie.  
Odpowiedź: x ∈ { 0, 2π,2π } 3

Wersja PDF