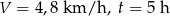/Szkoła średnia

Zadanie nr 3263109

Dodaj do ulubionych
Dodaj do rozwiązanych

Turysta przeszedł trasę długości 24 km ze stałą prędkością. Gdyby prędkość tę zwiększył o 1,2 km/h, to tę samą drogę przeszedłby w czasie o 1 godzinę krótszym. Oblicz rzeczywistą prędkość turysty i czas, w którym przebył trasę.

Rozwiązanie

Oznaczmy przez 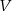V rzeczywista prędkość turysty i przez 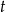t czas potrzebny na przejście trasy przy prędkości 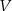V . Wówczas założenia możemy zapisać w postaci układu równań

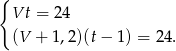
{ Vt = 2 4 (V + 1,2)(t − 1) = 24 .

Do drugiego równania podstawiamy 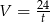24 V = -t

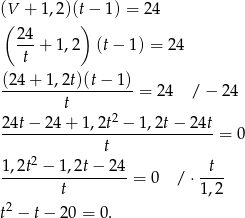
(V( + 1,2)(t)− 1) = 24 24 t--+ 1,2 (t− 1) = 24 (2-4+-1-,2t)(t−-1) t = 24 / − 2 4 2 4t− 24 + 1 ,2t2 − 1,2t − 24t ----------------------------- = 0 t 1-,2t2-−-1,2t-−-24 --t- t = 0 / ⋅1 ,2 2 t − t− 2 0 = 0.

Liczymy pierwiastki

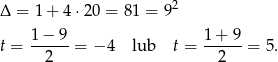
2 Δ = 1+ 4⋅2 0 = 81 = 9 1 − 9 1+ 9 t = ------= − 4 lub t = ------= 5. 2 2

Odrzucamy wynik ujemny. Zatem

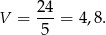
24- V = 5 = 4 ,8.

Turysta porusza się z prędkością 4,8 km/h, a przejście trasy zajmie mu 5 godzin.  
Odpowiedź: V = 4,8 km/h , t = 5 h

Wersja PDF