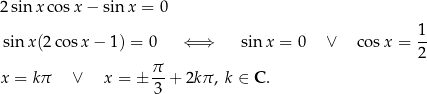Równania trygonometryczne w zasadzie nikomu się dobrze nie kojarzą. Powód jest prosty: na ogół mają nieskończenie wiele rozwiązań, więc samo zapisanie rozwiązań bywa kłopotliwe. Wykresy Rozwiązując równania/nierówności trygonometryczne nie do przecenienia są wykresy. Trzeba rozwiązać wiele przykładów, zanim będziemy umieli pisać rozwiązania równań/nierówności trygonometrycznych bez rysowania wykresu – na początku wykresy są niezbędne.
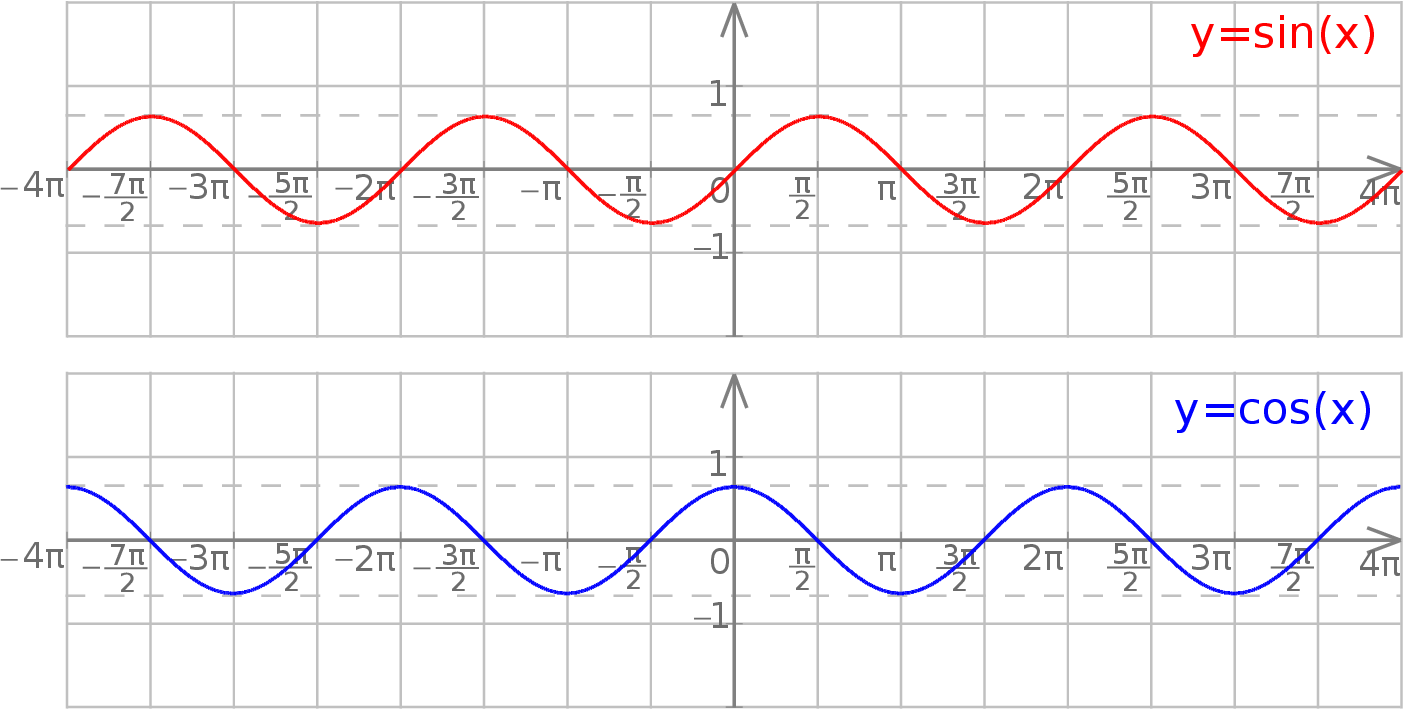
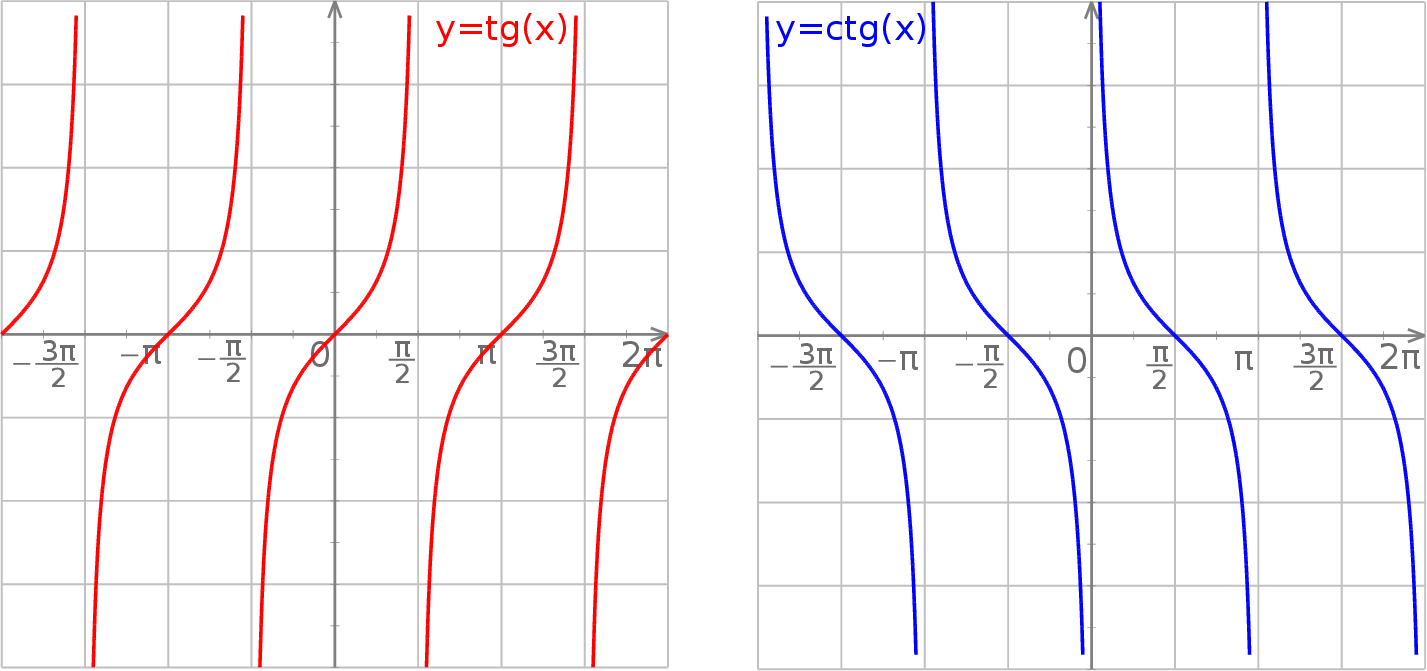
Oczywiście nie są nam potrzebne dokładne wykresy, na ogół wystarczy nam szkic. Najprostsze równania Bardzo wiele zadań sprowadza się do jednego ze wzorków:
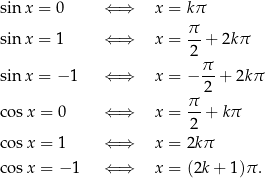
W każdym z powyższych wzorów literka 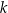 jest dowolną liczbą całkowitą, co zwykle krótko się zapisuje:
jest dowolną liczbą całkowitą, co zwykle krótko się zapisuje: 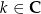 . Jak już wspominaliśmy, jest to typowa sytuacja w przypadku równań/nierówności trygonometrycznych – na ogół mają one nieskończenie wiele rozwiązań.
. Jak już wspominaliśmy, jest to typowa sytuacja w przypadku równań/nierówności trygonometrycznych – na ogół mają one nieskończenie wiele rozwiązań.
Jeżeli chodzi o same wzory, to radzę dobrze się im poprzyglądać i porównać je z wykresami odpowiednich funkcji. Wzory te opisują punkty, w których sinus/cosinus mają dołki i górki, oraz punkty, w których ich wykresy przecinają oś 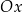 . Przed dalszą lekturą radzę na tyle się z tymi wzorkami oswoić, żeby umieć je wszystkie napisać nie zaglądając do powyższej listy. Oczywiście nie należy ich się uczyć na pamięć! – chodzi o umiejętność odczytywania ich z wykresów. W szczególności ważne jest, żeby rozumieć, dlaczego w niektórych jest
. Przed dalszą lekturą radzę na tyle się z tymi wzorkami oswoić, żeby umieć je wszystkie napisać nie zaglądając do powyższej listy. Oczywiście nie należy ich się uczyć na pamięć! – chodzi o umiejętność odczytywania ich z wykresów. W szczególności ważne jest, żeby rozumieć, dlaczego w niektórych jest 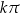 , a w innych
, a w innych 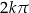 . Proste równania: tangens i cotangens Stosunkowo łatwe do rozwiązania są równania postaci
. Proste równania: tangens i cotangens Stosunkowo łatwe do rozwiązania są równania postaci 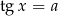 lub
lub 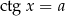 : jeżeli znamy chociaż jedną liczbę
: jeżeli znamy chociaż jedną liczbę 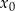 , która spełnia to równanie, to wszystkie rozwiązania są postaci
, która spełnia to równanie, to wszystkie rozwiązania są postaci 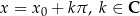 (funkcje te powtarzają się dokładnie co
(funkcje te powtarzają się dokładnie co 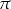 ).
).
A skąd wziąć 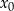 ? Jeżeli
? Jeżeli 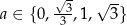 , to rozwiązanie
, to rozwiązanie 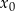 odczytujemy z tabelki
odczytujemy z tabelki
| kąt | 0 | 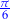 | 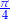 | 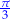 | 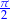 |
| tangens | 0 | 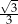 | 1 | 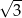 | 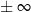 |
| cotangens | 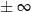 | 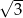 | 1 | 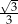 | 0 |
W przypadku wartości 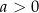 , których nie ma w powyższej tabelce, możemy co najwyżej odczytać z tablic przybliżoną wartość
, których nie ma w powyższej tabelce, możemy co najwyżej odczytać z tablic przybliżoną wartość 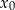 .
.
Jeżeli natomiast 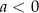 , to postępujemy podobnie jak wyżej, ale bierzemy
, to postępujemy podobnie jak wyżej, ale bierzemy 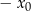 , gdzie
, gdzie 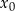 jest rozwiązaniem równania
jest rozwiązaniem równania 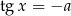 /
/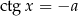 (to jest dobrze, bo
(to jest dobrze, bo 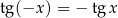 i
i 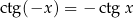 ).
).
Rozwiązania równania 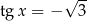 możemy zapisać w postaci
możemy zapisać w postaci 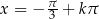 , gdzie
, gdzie 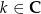 .
.
Rozwiążmy równanie 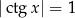 . Mamy
. Mamy
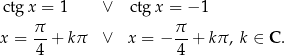
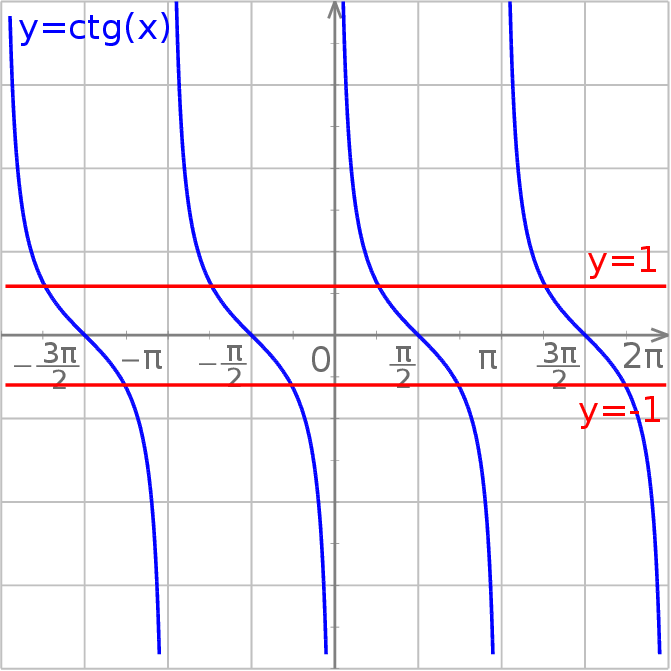
Proste równania: sinus i cosinus Odrobinę trudniej jest w przypadku funkcji sinus i cosinus. Jeżeli 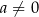 i
i 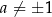 , to są dwa rodzaje rozwiązań równania
, to są dwa rodzaje rozwiązań równania 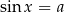 /
/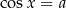 : jedne są na rosnących górkach, a drugie na malejących. Jeżeli mamy rozwiązania
: jedne są na rosnących górkach, a drugie na malejących. Jeżeli mamy rozwiązania 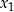 i
i 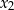 obu typów, to wszystkie rozwiązania są postaci
obu typów, to wszystkie rozwiązania są postaci 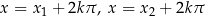 , gdzie
, gdzie 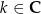 .
.
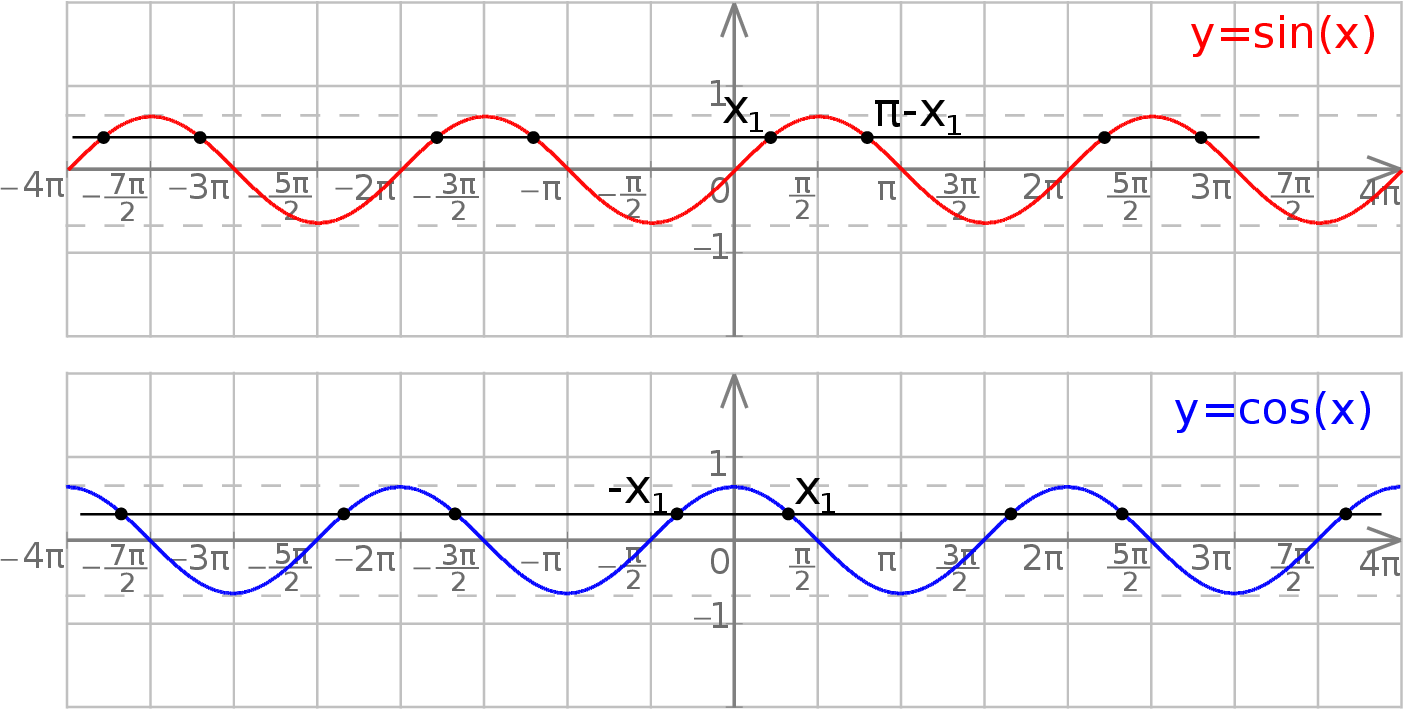
Zatem rozwiązywanie takiego równania sprowadza się do znalezienia jednego rozwiązania na rosnącej górce i jednego na malejącej.
Patrząc ponownie na wykresy sinusa i cosinusa, łatwo odczytać jak znaleźć drugie rozwiązanie 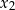 , gdy mamy
, gdy mamy 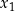 :
:
-
W przypadku cosinusa można zawsze wziąć
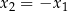 (bo
(bo 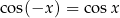 ). W tym przypadku często rozwiązanie równania zapisuje się w postaci
). W tym przypadku często rozwiązanie równania zapisuje się w postaci 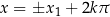 .
. -
Dla sinusa zwykle bierze się
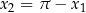 (bo
(bo 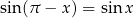 ) i wszystkie rozwiązania to
) i wszystkie rozwiązania to 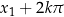 lub
lub 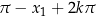 .
.
No dobrze, powiedzieliśmy już jak znaleźć 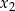 mając
mając 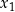 , ale skąd wziąć
, ale skąd wziąć 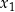 ?
?
Jeżeli 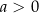 to zawsze możemy znaleźć rozwiązanie
to zawsze możemy znaleźć rozwiązanie 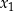 , które jest w przedziale
, które jest w przedziale 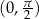 . Jeżeli
. Jeżeli 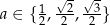 to rozwiązanie odczytujemy z tabelki
to rozwiązanie odczytujemy z tabelki
| kąt | 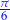 | 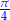 | 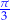 |
| sinus | 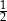 | 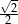 | 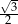 |
| cosinus | 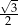 | 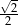 | 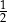 |
Rozwiązania równania 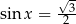 możemy zapisać w postaci:
możemy zapisać w postaci:
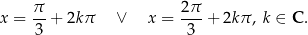
Rozwiązania równania 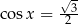 możemy zapisać w postaci:
możemy zapisać w postaci:
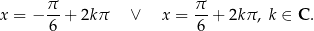
Możemy też zapisać je skrótowo 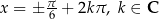 .
.
Jeżeli natomiast 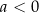 , to w przypadku funkcji
, to w przypadku funkcji  bierzemy
bierzemy 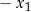 , gdzie
, gdzie 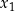 jest rozwiązaniem równania z prawą stroną równą
jest rozwiązaniem równania z prawą stroną równą 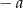 . W przypadku funkcji
. W przypadku funkcji 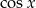 bierzemy
bierzemy 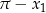 .
.
Rozwiązania równania 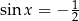 to
to
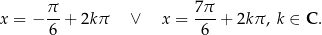
Równie dobrze możemy wziąć
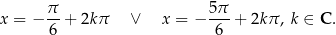
Rozwiązaniem równania 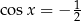 jest zbiór
jest zbiór 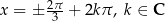 .
.
Jak to zapamiętać? Zanim przejdziemy dalej, warto na chwilę się zatrzymać i pozbierać to, co do tej pory ustaliliśmy. Rozwiązanie równania 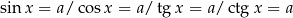 zawsze sprowadza się do pytania: w jakich punktach prosta
zawsze sprowadza się do pytania: w jakich punktach prosta 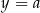 przecina wykres odpowiedniej funkcji. Jak te punkty znaleźć? – oczywiście trzeba naszkicować wykres funkcji i odczytać z wykresu. Zamiast uczyć się na pamięć wyżej wypisanych reguł, wystarczy zapamiętać, że w przypadku sinusa/cosinusa i
przecina wykres odpowiedniej funkcji. Jak te punkty znaleźć? – oczywiście trzeba naszkicować wykres funkcji i odczytać z wykresu. Zamiast uczyć się na pamięć wyżej wypisanych reguł, wystarczy zapamiętać, że w przypadku sinusa/cosinusa i  są dwa rodzaje rozwiązań, a we wszystkich pozostałych przypadkach wystarczy znaleźć jedno rozwiązanie i skorzystać z okresowości odpowiedniej funkcji. W każdym z przypadków, wszystko co jest nam potrzebne do napisania rozwiązań znajdziemy na wykresie. Proste nierówności Jeżeli umiemy już rozwiązywać równania postaci
są dwa rodzaje rozwiązań, a we wszystkich pozostałych przypadkach wystarczy znaleźć jedno rozwiązanie i skorzystać z okresowości odpowiedniej funkcji. W każdym z przypadków, wszystko co jest nam potrzebne do napisania rozwiązań znajdziemy na wykresie. Proste nierówności Jeżeli umiemy już rozwiązywać równania postaci 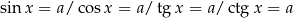 , to rozwiązywanie analogicznych nierówności nie powinno sprawiać żadnego problemu. Nie będziemy tu wypisywać regułek ani wzorków, bo to nie ma sensu – zawsze rysujemy obrazek i patrzymy na nim o co chodzi.
, to rozwiązywanie analogicznych nierówności nie powinno sprawiać żadnego problemu. Nie będziemy tu wypisywać regułek ani wzorków, bo to nie ma sensu – zawsze rysujemy obrazek i patrzymy na nim o co chodzi.
Rozwiążmy nierówność 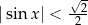 .
.
Dana nierówność jest równoważna nierówności
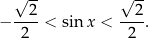
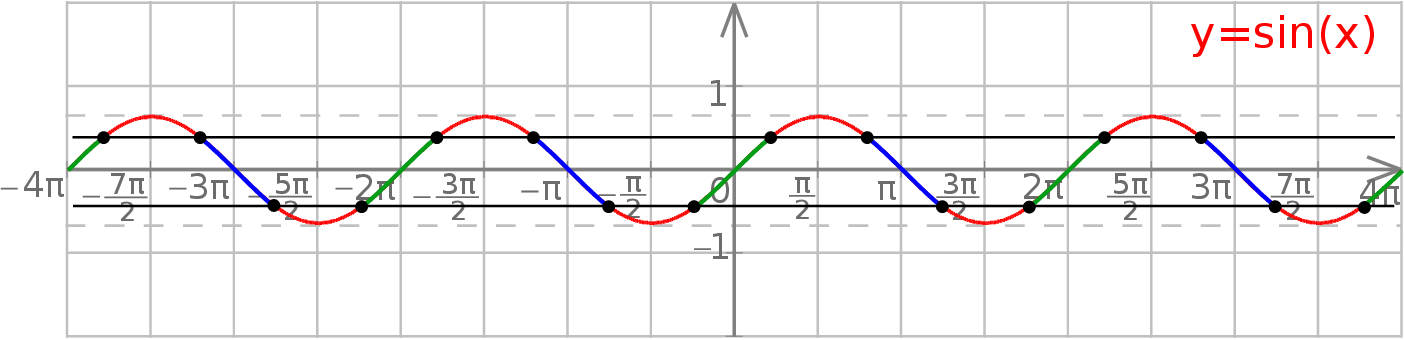
Szukamy zatem na wykresie przedziałów, na których sinus jest w przedziale 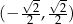 . Gdy się przyjrzymy, to widać, że są dwa rodzaje takich przedziałów: zielone i niebieskie. Ponieważ umiemy już rozwiązywać równanie
. Gdy się przyjrzymy, to widać, że są dwa rodzaje takich przedziałów: zielone i niebieskie. Ponieważ umiemy już rozwiązywać równanie 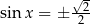 , nie jest trudno opisać te przedziały, są to
, nie jest trudno opisać te przedziały, są to
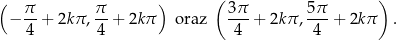
Bardziej skomplikowane równania/nierówności Rozwiązywanie ogólnych równań trygonometrycznych prawie zawsze polega na przekształcaniu równania/nierówności do postaci, w której pozostają nam do rozwiązania proste równania/nierówności, o których pisaliśmy wyżej. Jak to robić? Na tym polega cała zabawa – do tego trzeba mieć dobrze opanowaną umiejętność posługiwania się tożsamościami trygonometrycznymi. Można wyróżnić dwie najważniejsze metody postępowania.
1. Przekształcamy dane równanie/nierówność tak, aby występowała w nim tylko jedna funkcja trygonometryczna. Możemy wtedy za nią podstawić i otrzymamy równanie/nierówność bez funkcji trygonometrycznych.
Rozwiążmy równanie 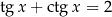 .
.
Ponieważ 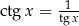 , możemy podstawić
, możemy podstawić 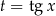 , co daje nam równanie
, co daje nam równanie
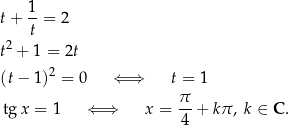
Rozwiążmy nierówność 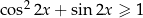 .
.
Korzystamy z jedynki trygonometrycznej i podstawiamy 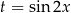 .
.
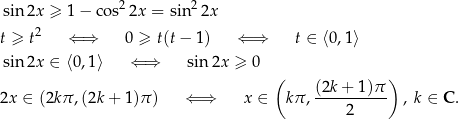
2. Inny popularny sposób, to przekształcenie równania/nierówności do postaci, w której z lewej strony mamy iloczyn prostych wyrażeń, a z prawej strony 0.
Rozwiążmy równanie 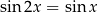 .
.
Przekształcamy