/Szkoła średnia

Zadanie nr 3962726

Dodaj do ulubionych
Dodaj do rozwiązanych

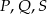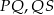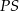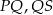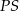Punkty P ,Q ,S dzielą okrąg na trzy łuki PQ ,QS i P S . Długości łuków P Q ,QS i PS pozostają w stosunku 1:2:3. Oblicz miary kątów trójkąta P QS .

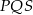Rozwiązanie

Zaczynamy od rysunku

PIC

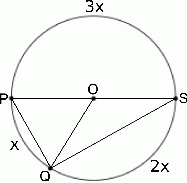
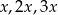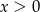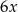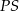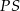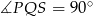Z podanych informacji wynika, że łuki na które został podzielny okrąg mają długości: x,2x ,3x dla pewnego x > 0 . Cały okrąg ma więc długość 6x . To oznacza, że łuk P S to połowa okręgu, czyli odcinek PS jest średnicą. Zatem ∘ ∡P QS = 90 .

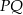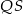Kąty środkowe odpowiadające łukom PQ i QS są odpowiednio równe

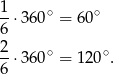
1-⋅36 0∘ = 60∘ 6 2- ∘ ∘ 6 ⋅36 0 = 120 .

Ponieważ kąt wpisany jest równy połowie kąta środkowego opartego na tym samym łuku, to kąty ostre trójkąta 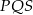P QS wynoszą 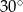30 ∘ i 60∘ .  
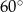Odpowiedź: ∘ ∘ ∘ 30 ,6 0 ,90

Wersja PDF