/Szkoła średnia

Egzamin Maturalny
z Matematyki poziom rozszerzony
stara formuła 9 maja 2017 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Rozwiąż nierówność 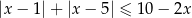|x − 1|+ |x − 5 | ≤ 1 0− 2x .

Zadanie 2
(5 pkt)

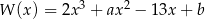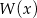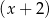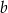Dany jest wielomian W (x) = 2x3 + ax2 − 13x + b . Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu W (x) przez (x + 2) jest równa 20. Oblicz współczynniki a i b oraz pozostałe pierwiastki wielomianu W (x) .

Zadanie 3
(5 pkt)

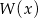Wyznacz wszystkie wartości parametru 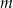m , dla których równanie

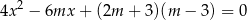
2 4x − 6mx + (2m + 3)(m − 3) = 0

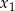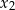ma dwa różne rozwiązania rzeczywiste x 1 i x2 , przy czym 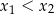x 1 < x2 , spełniające warunek

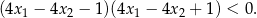
(4x 1 − 4x 2 − 1 )(4x 1 − 4x2 + 1) < 0.

Zadanie 4
(6 pkt)

Liczby 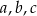a,b,c są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa 27. Ciąg 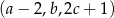(a− 2 ,b,2c+ 1) jest geometryczny. Wyznacz liczby a,b,c .

Zadanie 5
(3 pkt)

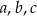Udowodnij, że dla dowolnych różnych liczb rzeczywistych 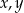x ,y prawdziwa jest nierówność

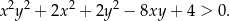
x2y2 + 2x 2 + 2y 2 − 8xy + 4 > 0.

Zadanie 6
(3 pkt)

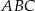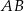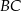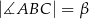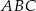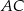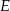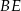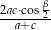W trójkącie ostrokątnym ABC bok AB ma długość c , długość boku BC jest równa a oraz |∡ABC | = β . Dwusieczna kąta ABC przecina bok AC trójkąta w punkcie E . Wykaż, że długość odcinka BE jest równa 2ac⋅cos β --a+c-2 .

Zadanie 7
(4 pkt)

Oblicz, ile jest liczb sześciocyfrowych, w których zapisie nie występuje zero, natomiast występują dwie dziewiątki, jedna szóstka i suma wszystkich cyfr jest równa 30.

Zadanie 8
(3 pkt)

W dwóch pudełkach umieszczono po pięć kul, przy czym w pierwszym pudełku: 2 kule białe i 3 kule czerwone, a w drugim pudełku: 1 kulę białą i 4 kule czerwone. Z pierwszego pudełka losujemy jedną kulę i bez oglądania wkładamy ją do drugiego pudełka. Następnie losujemy jedną kulę z drugiego pudełka. Oblicz prawdopodobieństwo wylosowania kuli białej z drugiego pudełka.

Zadanie 9
(6 pkt)

W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.

Zadanie 10
(6 pkt)

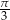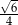Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka tworzą z jego podstawą kąty o miarach π 3- i α . Cosinus kąta między tymi przekątnymi jest równy √- -6- 4 . Wyznacz miarę kąta α .

Zadanie 11
(5 pkt)

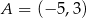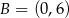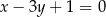Wyznacz równanie okręgu przechodzącego przez punkty A = (− 5,3) i B = (0,6) , którego środek leży na prostej o równaniu x − 3y + 1 = 0 .

Arkusz Wersja PDF
Rozwiązania