/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 27 lutego 2016 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 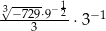 jest równa
jest równa
A) 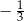 B)
B) 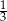 C) 1 D)
C) 1 D) 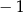
Jeżeli 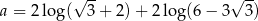 to
to 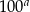 jest liczbą
jest liczbą
A) ujemną B) nieparzystą C) niewymierną D) parzystą
Kwotę 1000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 4% w stosunku rocznym. Po każdym kwartale środki zgromadzone na lokacie są powiększane o odsetki, od których odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa
A) 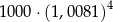 B)
B) 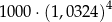 C)
C) 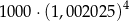 D)
D) 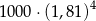
Wyrażenie 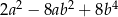 może być przekształcone do postaci
może być przekształcone do postaci
A) 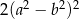 B)
B) 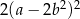 C)
C) 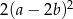 D)
D) 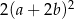
Iloczyn dwóch liczb dodatnich, z których jedna jest o 11 większa od drugiej jest równy 350. Suma tych liczb jest równa
A) 39 B) 14 C) 25 D) 37
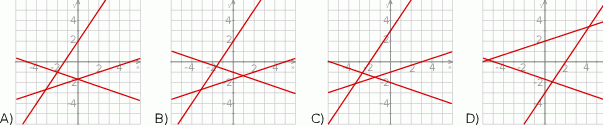
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań 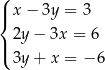 Wskaż ten rysunek.
Wskaż ten rysunek.
Równanie 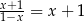
A) ma dokładnie jedno rozwiązanie: 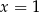 .
.
B) ma dokładnie dwa rozwiązania: 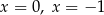 .
.
C) ma dokładnie jedno rozwiązanie: 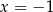 .
.
D) ma dokładnie jedno rozwiązanie: 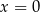 .
.
Wyrażenie 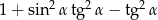 może być przekształcone do postaci
może być przekształcone do postaci
A) 1 B) 0 C) 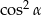 D)
D) 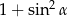
Suma kwadratów czterech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 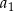 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 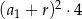 B)
B) 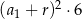 C)
C) 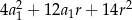 D)
D) 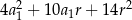
Wykresy funkcji 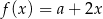 i
i 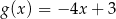 przecinają oś
przecinają oś 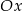 w dwóch różnych punktach. Stąd wynika, że
w dwóch różnych punktach. Stąd wynika, że
A) 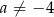 B)
B) 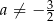 C)
C) 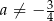 D)
D) 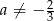
Funkcja 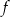 jest określona wzorem
jest określona wzorem 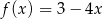 dla każdej liczby z przedziału
dla każdej liczby z przedziału 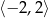 . Zbiorem wartości tej funkcji jest przedział
. Zbiorem wartości tej funkcji jest przedział
A) 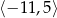 B)
B) 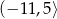 C)
C) 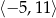 D)
D) 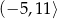
Wierzchołek paraboli będącej wykresem funkcji kwadratowej 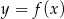 ma współrzędne
ma współrzędne 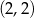 . Wówczas wierzchołek paraboli będącej wykresem funkcji
. Wówczas wierzchołek paraboli będącej wykresem funkcji 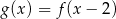 ma współrzędne
ma współrzędne
A) 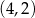 B)
B) 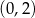 C)
C) 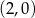 D)
D) 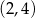
Ciąg geometryczny 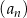 jest określony wzorem
jest określony wzorem 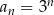 dla
dla 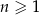 . Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 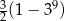 B)
B) 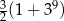 C)
C) 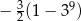 D)
D) 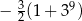
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
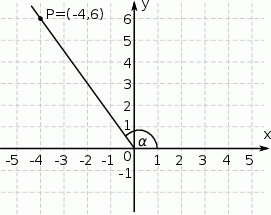
A) 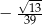 B)
B) 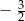 C)
C) 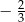 D)
D) 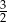
Na prostej o równaniu 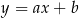 leżą punkty
leżą punkty 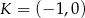 i
i 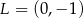 . Wynika stąd, że
. Wynika stąd, że
A) 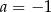 i
i 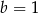 B)
B) 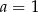 i
i 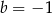 C)
C) 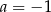 i
i 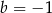 D)
D) 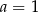 i
i 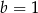
W trójkącie 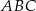 , w którym
, w którym 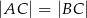 , na boku
, na boku 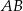 wybrano punkt
wybrano punkt 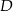 taki, że
taki, że 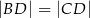 oraz
oraz 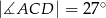 (zobacz rysunek).
(zobacz rysunek).
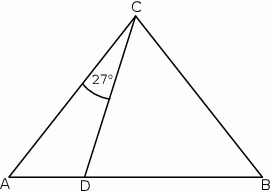
Wynika stąd, że kąt 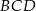 ma miarę
ma miarę
A) 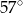 B)
B) 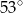 C)
C) 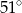 D)
D) 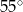
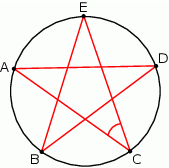
Punkty 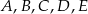 okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 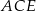 jest równa
jest równa
A) 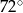 B)
B) 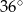 C)
C) 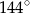 D)
D) 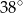
Prosta 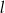 o równaniu
o równaniu 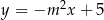 jest równoległa do prostej
jest równoległa do prostej 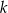 o równaniu
o równaniu 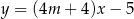 . Zatem
. Zatem
A) 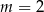 B)
B) 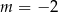 C)
C) 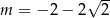 D)
D) 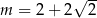
Pole równoległoboku o bokach długości 6 i 8 oraz kącie rozwartym 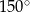 jest równe
jest równe
A) 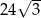 B) 48 C)
B) 48 C) 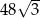 D) 24
D) 24
Punkt 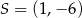 jest środkiem odcinka
jest środkiem odcinka 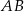 , gdzie
, gdzie 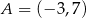 i
i 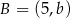 . Wtedy
. Wtedy
A) 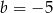 B)
B) 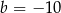 C)
C) 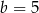 D)
D) 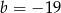
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 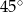 , a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
, a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
A) 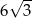 B) 9 C) 12 D)
B) 9 C) 12 D) 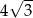
Przekrojem osiowym stożka o objętości 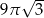 jest trójkąt równoboczny. Obwód tego trójkąta jest równy
jest trójkąt równoboczny. Obwód tego trójkąta jest równy
A) 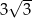 B)
B) 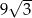 C) 18 D) 6
C) 18 D) 6
Średnia arytmetyczna wszystkich wyrazów 100-wyrazowego ciągu arytmetycznego 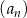 jest równa 37, a różnica tego ciągu jest równa
jest równa 37, a różnica tego ciągu jest równa 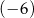 . Pierwszy wyraz ciągu
. Pierwszy wyraz ciągu 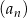 jest równy
jest równy
A) 594 B) 520 C) 260 D) 334
Liczba sześcianów liczb całkowitych w zbiorze kolejnych liczb naturalnych
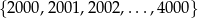
jest równa
A) 3 B) 4 C) 5 D) 8
Na loterię przygotowano pulę 200 losów, w tym 4 wygrywające. Po wylosowaniu pewnej liczby losów, wśród których były dokładnie dwa wygrywające, szansa na wygraną była taka sama jak przed rozpoczęciem loterii. Stąd wynika, że wylosowano
A) 8 losów. B) 40 losów. C) 100 losów. D) 50 losów.
Zadania otwarte
Rozwiąż równanie 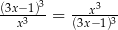 , gdzie
, gdzie 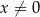 i
i 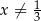 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 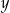 prawdziwa jest nierówność
prawdziwa jest nierówność 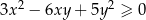 .
.
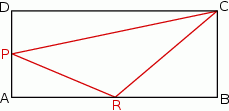
W prostokącie 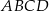 punkt
punkt 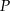 jest środkiem boku
jest środkiem boku 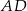 , a punkt
, a punkt 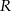 jest środkiem boku
jest środkiem boku 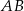 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 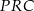 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 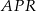 oraz
oraz 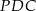 .
.
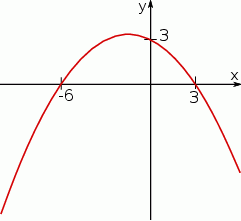
Na podstawie przedstawionego fragmentu wykresu funkcji kwadratowej wyznacz jej wzór.
Liczby 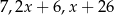 w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę
w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę  tego ciągu.
tego ciągu.
Każdy z trojga chłopców pomyślał sobie liczbę dwucyfrową. Jakie jest prawdopodobieństwo, że żadne dwie z tych osób nie pomyślały tej samej liczby? Wynik podaj w postaci ułamka nieskracalnego.
Wyznacz równanie symetralnej przeciwprostokątnej trójkąta prostokątnego o wierzchołkach 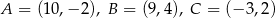 .
.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 16. Krawędź boczna jest nachylona do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy 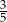 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
Wojtek ułożył z drewnianych sześciennych klocków kwadrat (kładąc klocki jeden obok drugiego) i zostały mu 23 klocki. Następnie spróbował ułożyć kwadrat o boku o 1 klocek większym niż poprzedni i zabrakło mu 8 klocków. Ile klocków miał Wojtek?