/Szkoła średnia

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 26 kwietnia 2014 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Na rysunku przedstawiony jest fragment wykresu funkcji określonej wzorem 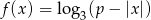f(x) = log 3(p− |x|) .

PIC

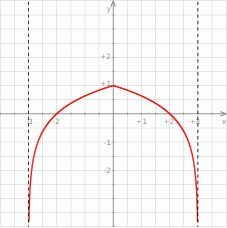
  • Podaj wartość p .
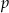  • Naszkicuj wykres funkcji y = |f(x )| .
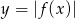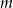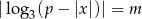  • Podaj w zależności od parametru m liczbę rozwiązań równania |log3(p − |x|)| = m .

Zadanie 2
(4 pkt)

Wyznacz najmniejszą i największą wartość funkcji 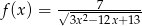f(x) = √---2-7----- 3x −12x+13 na przedziale ⟨0,6⟩ .

Zadanie 3
(4 pkt)

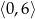Dla jakich wartości 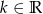k ∈ R równanie 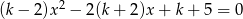(k− 2)x2 − 2(k + 2)x + k + 5 = 0 ma dwa różne pierwiastki dodatnie?

Zadanie 4
(4 pkt)

Wykaż, że jeżeli 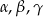α,β,γ są kątami trójkąta, to

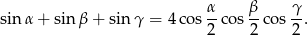
α- β- γ- sinα + sin β + sin γ = 4co s2 cos 2 cos 2.

Zadanie 5
(5 pkt)

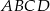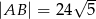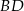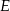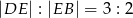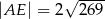Dany jest prostokąt ABCD , w którym √ -- |AB | = 24 5 . Na przekątnej BD leży punkt E taki, że |DE | : |EB | = 3 : 2 oraz √ ---- |AE | = 2 269 . Oblicz pole prostokąta ABCD .

Zadanie 6
(4 pkt)

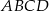Równanie 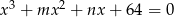3 2 x + mx + nx + 6 4 = 0 ma trzy pierwiastki będące kolejnymi wyrazami ciągu geometrycznego o ilorazie 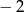− 2 . Wyznacz 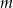m i n .

Zadanie 7
(4 pkt)

Wykaż, że styczne do okręgu 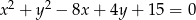x2 + y2 − 8x + 4y + 15 = 0 poprowadzone przez punkt 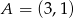A = (3,1 ) są prostopadłe.

Zadanie 8
(4 pkt)

Rozwiąż równanie 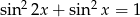sin 22x + sin2x = 1 w zbiorze ⟨0,2π ⟩ .

Zadanie 9
(4 pkt)

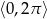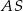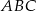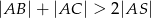Odcinek AS jest środkową trójkąta ABC . Udowodnij, że |AB |+ |AC | > 2|AS | .

Zadanie 10
(3 pkt)

Korzystając z tego, że 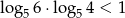lo g 6 ⋅log 4 < 1 5 5 wykaż, że

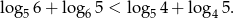
log 6 + log 5 < log 4+ lo g 5. 5 6 5 4

Zadanie 11
(5 pkt)

Dany jest ostrosłup prawidłowy czworokątny 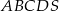ABCDS o podstawie 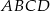ABCD . Pole trójkąta 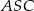ASC jest równe 120, a stosunek długości podstawy tego trójkąta do długości ramienia jest równy 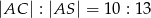|AC | : |AS | = 10 : 13 . Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

Zadanie 12
(5 pkt)

Grupę 12 uczniów, wśród których jest 6 dziewczynek i 6 chłopców podzielono na 3 równoliczne grupy. Oblicz prawdopodobieństwo tego, że w każdej z utworzonych grup będzie tyle samo dziewcząt.

Arkusz Wersja PDF
Rozwiązania