/Szkoła średnia
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy 4 czerwca 2019 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem równania 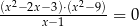 nie jest liczba
nie jest liczba
A) 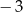 B)
B) 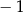 C) 1 D) 3
C) 1 D) 3
Liczba 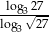 jest równa
jest równa
A) 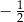 B) 2 C)
B) 2 C) 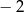 D)
D) 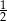
Jedną z liczb spełniających nierówność 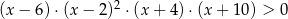 jest
jest
A) 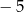 B) 0 C) 3 D) 5
B) 0 C) 3 D) 5
Liczba dodatnia  jest zapisana w postaci ułamka zwykłego. Jeżeli licznik tego ułamka zmniejszymy o 50%, a jego mianownik zwiększymy o 50%, to otrzymamy liczbę
jest zapisana w postaci ułamka zwykłego. Jeżeli licznik tego ułamka zmniejszymy o 50%, a jego mianownik zwiększymy o 50%, to otrzymamy liczbę 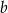 taką, że
taką, że
A) 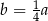 B)
B) 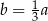 C)
C) 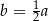 D)
D) 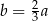
Funkcja liniowa 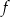 jest określona wzorem
jest określona wzorem 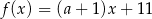 , gdzie
, gdzie  to pewna liczba rzeczywista, ma miejsce zerowe równe
to pewna liczba rzeczywista, ma miejsce zerowe równe 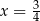 . Stąd wynika, że
. Stąd wynika, że
A) 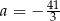 B)
B) 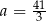 C)
C) 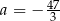 D)
D) 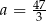
Funkcja 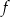 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 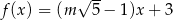 . Ta funkcja jest rosnąca dla każdej liczby
. Ta funkcja jest rosnąca dla każdej liczby 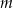 spełniającej warunek
spełniającej warunek
A) 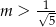 B)
B) 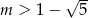 C)
C) 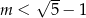 D)
D) 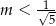
Układ równań 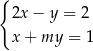 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 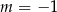 B)
B) 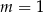 C)
C) 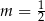 D)
D) 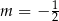
Rysunek przedstawia wykres funkcji 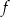 zbudowany z 6 odcinków, przy czym punkty
zbudowany z 6 odcinków, przy czym punkty 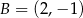 i
i 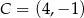 należą do wykresu funkcji.
należą do wykresu funkcji.
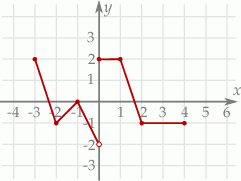
Równanie 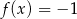 ma
ma
A) dokładnie jedno rozwiązanie. B) dokładnie dwa rozwiązania.
C) dokładnie trzy rozwiązania. D) nieskończenie wiele rozwiązań.
Dany jest rosnący ciąg arytmetyczny 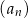 , określony dla liczb naturalnych
, określony dla liczb naturalnych 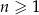 , o wyrazach dodatnich. Jeśli
, o wyrazach dodatnich. Jeśli 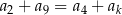 , to
, to 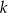 jest równe
jest równe
A) 8 B) 7 C) 6 D) 5
W ciągu 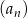 określonym dla każdej liczby
określonym dla każdej liczby 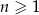 jest spełniony warunek
jest spełniony warunek 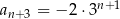 . Wtedy
. Wtedy
A) 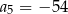 B)
B) 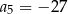 C)
C) 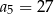 D)
D) 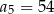
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 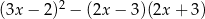 jest po uproszczeniu równe
jest po uproszczeniu równe
A) 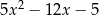 B)
B) 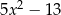 C)
C) 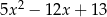 D)
D) 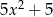
Kąt 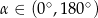 oraz wiadomo, że
oraz wiadomo, że 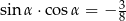 . Wartość wyrażenia
. Wartość wyrażenia 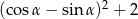 jest równa
jest równa
A) 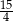 B)
B)  C)
C) 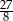 D)
D) 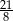
Wartość wyrażenia 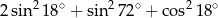 jest równa
jest równa
A) 0 B) 1 C) 2 D) 4
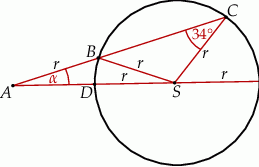
Punkty 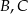 i
i 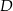 leżą na okręgu o środku
leżą na okręgu o środku 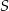 i promieniu
i promieniu  . Punkt
. Punkt 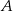 jest punktem wspólnym prostych
jest punktem wspólnym prostych 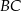 i
i 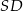 , a odcinki
, a odcinki 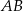 i
i 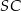 są równej długości. Miara kąta
są równej długości. Miara kąta 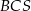 jest równa
jest równa 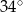 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A) 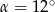 B)
B) 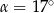 C)
C) 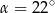 D)
D) 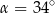
Pole trójkąta 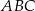 o wierzchołkach
o wierzchołkach 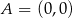 ,
, 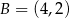 ,
, 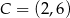 jest równe
jest równe
A) 5 B) 10 C) 15 D) 20
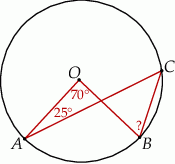
Na okręgu o środku w punkcie 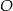 wybrano trzy punkty
wybrano trzy punkty 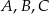 tak, że
tak, że 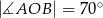 ,
, 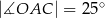 . Cięciwa
. Cięciwa 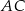 przecina promień
przecina promień 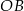 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara 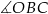 jest równa
jest równa
A) 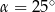 B)
B) 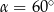 C)
C) 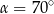 D)
D) 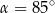
W układzie współrzędnych na płaszczyźnie dany jest odcinek 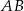 o końcach w punktach
o końcach w punktach 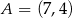 ,
, 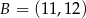 . Punkt
. Punkt 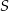 leży wewnątrz odcinka
leży wewnątrz odcinka 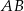 oraz
oraz 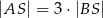 . Wówczas
. Wówczas
A) 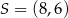 B)
B) 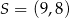 C)
C) 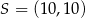 D)
D) 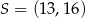
Suma odległości punktu 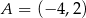 od prostych o równaniach
od prostych o równaniach 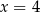 i
i 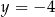 jest równa
jest równa
A) 14 B) 12 C) 10 D) 8
Suma długości wszystkich krawędzi sześcianu jest równa 96 cm. Pole powierzchni całkowitej tego sześcianu jest równe
A) 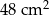 B)
B) 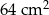 C)
C) 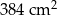 D)
D) 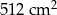
Dany jest trójkąt równoramienny 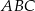 , w którym
, w którym 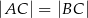 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę 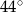 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 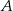 przecina bok
przecina bok 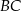 tego trójkąta w punkcie
tego trójkąta w punkcie 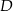 . Kąt
. Kąt 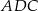 ma miarę
ma miarę
A) 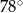 B)
B) 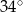 C)
C) 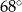 D)
D) 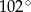
Liczb naturalnych dwucyfrowych podzielnych przez 6 jest
A) 60 B) 45 C) 30 D) 15
Podstawą ostrosłupa jest kwadrat 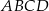 o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna 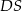 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
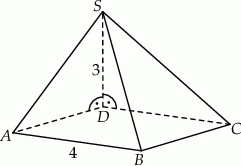
Pole ściany 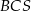 tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 20 B) 10 C) 16 D) 12
Dany jest sześcian 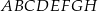 . Przekątne
. Przekątne 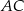 i
i 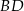 ściany
ściany 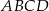 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 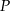 (zobacz rysunek).
(zobacz rysunek).
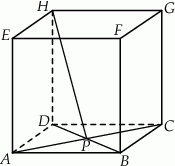
Tangens kąta, jaki odcinek 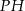 tworzy z płaszczyzną
tworzy z płaszczyzną 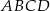 , jest równy
, jest równy
A) 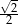 B)
B) 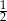 C) 1 D)
C) 1 D) 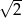
Przekrojem osiowym walca jest kwadrat o przekątnej długości 12 . Objętość tego walca jest zatem równa
A) 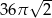 B)
B) 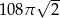 C)
C) 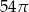 D)
D) 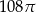
Ze zbioru kolejnych liczb naturalnych 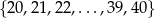 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
A) 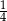 B)
B) 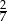 C)
C) 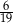 D)
D) 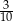
Zadania otwarte
Rozwiąż nierówność 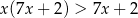 .
.
Wyznacz wszystkie liczby rzeczywiste  , które spełniają warunek:
, które spełniają warunek: 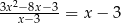 .
.
Dany jest trójkąt 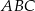 . Punkt
. Punkt 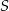 jest środkiem boku
jest środkiem boku 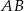 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 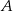 i
i 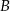 od prostej
od prostej 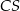 są równe.
są równe.
Wykaż, że dla każdej liczby 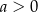 i dla każdej liczby
i dla każdej liczby 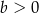 prawdziwa jest nierówność
prawdziwa jest nierówność
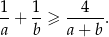
W ciągu geometrycznym przez 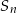 oznaczamy sumę
oznaczamy sumę  początkowych wyrazów tego ciągu, dla liczb naturalnych
początkowych wyrazów tego ciągu, dla liczb naturalnych 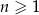 . Wiadomo, że dla pewnego ciągu geometrycznego:
. Wiadomo, że dla pewnego ciągu geometrycznego: 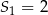 i
i 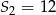 . Wyznacz iloraz i piąty wyraz tego ciągu.
. Wyznacz iloraz i piąty wyraz tego ciągu.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy sumę oczek równą 16.
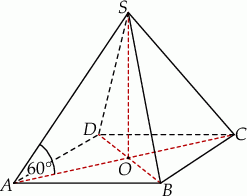
Podstawą ostrosłupa 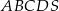 jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy
jest prostokąt o polu równym 432, a stosunek długości boków tego prostokąta jest równy 3:4. Przekątne podstawy 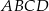 przecinają się w punkcie
przecinają się w punkcie 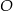 . Odcinek
. Odcinek 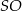 jest wysokością ostrosłupa (zobacz rysunek). Kąt
jest wysokością ostrosłupa (zobacz rysunek). Kąt 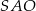 ma miarę
ma miarę 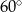 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Liczby rzeczywiste  i
i  spełniają warunek
spełniają warunek 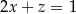 . Wyznacz takie wartości
. Wyznacz takie wartości  i
i  , dla których wyrażenie
, dla których wyrażenie 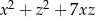 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
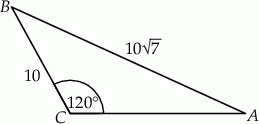
Dany jest trójkąt rozwartokątny 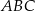 , w którym
, w którym 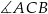 ma miarę
ma miarę 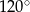 . Ponadto wiadomo, że
. Ponadto wiadomo, że 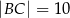 i
i 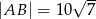 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 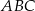 .
.