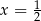/Szkoła średnia

Zadanie nr 4646031

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 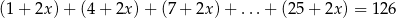(1+ 2x)+ (4+ 2x) + (7 + 2x) + ...+ (2 5+ 2x) = 126 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.

Rozwiązanie

Widać, że ciąg z lewej strony równania jest ciągiem arytmetycznym o różnicy 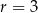r = 3 . Zatem ze wzoru n –ty wyraz ciągu mamy

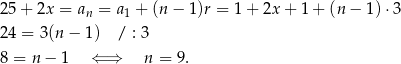
25 + 2x = an = a1 + (n − 1)r = 1+ 2x+ 1+ (n− 1)⋅3 24 = 3(n − 1) / : 3 8 = n− 1 ⇐ ⇒ n = 9.

Zatem z lewej strony równania jest 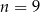n = 9 składników i ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego mamy

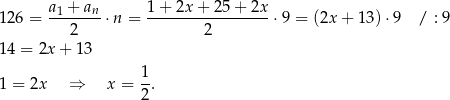
126 = a1 +-an⋅ n = 1-+-2x-+-2-5+--2x ⋅9 = (2x + 13 )⋅9 / : 9 2 2 14 = 2x + 13 1 = 2x ⇒ x = 1-. 2

 
Odpowiedź: x = 1 2

Wersja PDF