/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 7 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 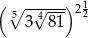 jest równa
jest równa
A) 3 B) 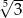 C)
C) 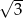 D) 9
D) 9
Ile liczb wymiernych znajduje się w zbiorze
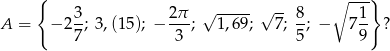
A) 3 B) 4 C) 5 D) 6
Pole kwadratu 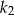 jest o 21% większe od pola kwadratu
jest o 21% większe od pola kwadratu 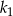 . Wówczas długość boku kwadratu
. Wówczas długość boku kwadratu 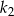 jest większa od długości boku kwadratu
jest większa od długości boku kwadratu 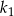 o
o
A) 10% B) 110% C) 21% D) 121%
Liczba 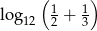 jest równa
jest równa
A) 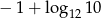 B) 10 C)
B) 10 C) 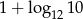 D)
D) 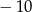
Zbiór rozwiązań nierówności 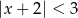 jest taki sam jak zbiór rozwiązań nierówności
jest taki sam jak zbiór rozwiązań nierówności
A) 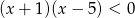
B) 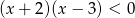
C) 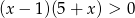
D) 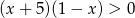
Liczby 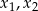 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 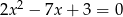 . Iloczyn
. Iloczyn 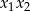 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 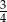
Jeżeli 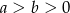 to wyrażenie
to wyrażenie 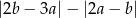 jest równe
jest równe
A) 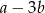 B)
B) 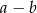 C)
C) 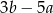 D)
D) 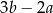
Liczba pierwiastków rzeczywistych wielomianu 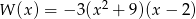 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Dane są funkcje 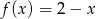 oraz
oraz 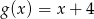 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 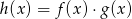 .
.
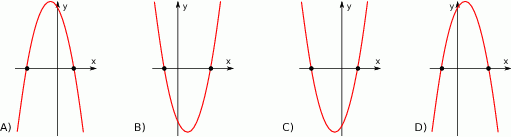
Wskaż 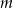 , dla którego funkcja liniowa
, dla którego funkcja liniowa 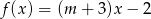 jest malejąca
jest malejąca
A) 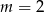 B)
B) 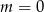 C)
C) 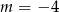 D)
D) 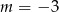
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 8 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 4. Przeciwprostokątna tego trójkąta ma długość
A) 20 B) 16 C) 8 D) 18
Iloczyn wielomianów 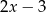 oraz
oraz 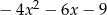 jest równy
jest równy
A) 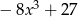 B)
B) 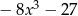 C)
C) 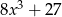 D)
D) 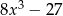
Ciąg 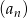 dany jest wzorem,
dany jest wzorem, 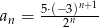 . Ciąg
. Ciąg 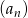 jest ciągiem
jest ciągiem
A) rosnącym B) malejącym C) arytmetycznym D) geometrycznym
Na rysunku przedstawiony jest wykres funkcji 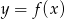 .
.
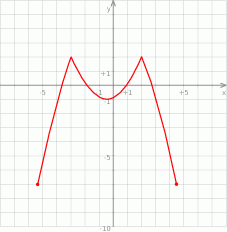
Które z równań ma dokładnie trzy rozwiązania?
A) 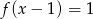 B)
B) 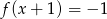 C)
C) 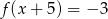 D)
D) 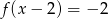
Przez wierzchołek 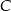 trójkąta prostokątnego
trójkąta prostokątnego 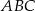 poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie.
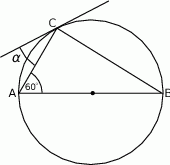
Jeżeli 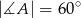 to miara kąta
to miara kąta  jest równa
jest równa
A) 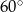 B)
B) 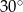 C)
C) 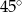 D)
D) 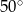
Kąt  jest ostry oraz
jest ostry oraz 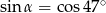 . Wtedy miara kąta
. Wtedy miara kąta  jest równa:
jest równa:
A) 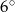 B)
B) 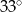 C)
C) 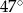 D)
D) 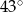
Promień okręgu o równaniu 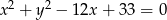 ma długość
ma długość
A) 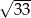 B)
B) 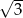 C) 3 D) 6
C) 3 D) 6
Wiadomo, że dziedziną funkcji 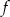 określonej wzorem
określonej wzorem 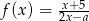 jest zbiór
jest zbiór 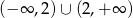 . Wówczas
. Wówczas
A) 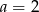 B)
B) 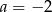 C)
C) 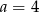 D)
D) 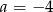
Które z równań należy wpisać w miejsce gwiazdek, aby układ równań 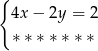 miał nieskończenie wiele rozwiązań?
miał nieskończenie wiele rozwiązań?
A) 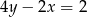 B)
B) 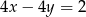 C)
C) 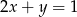 D)
D) 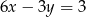
Ciąg 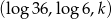 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 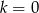 B)
B) 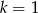 C)
C) 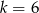 D)
D) 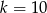
Pole powierzchni bocznej stożka wynosi 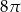 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 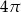 B)
B) 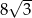 C)
C) 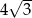 D)
D) 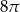
Wyniki konkursu ortograficznego podano w punktach: 82, 94, 88, 92, 90, 86, 76, 72. Medianą tego zestawu wyników jest
A) 86 B) 88 C) 87 D) 90
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania liczby oczek różnej od 5 jest równe
A) 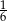 B)
B) 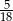 C)
C) 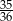 D)
D) 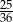
Zadania otwarte
Rozwiąż nierówność 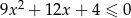 .
.
Oblicz sumę wszystkich liczb trzycyfrowych, których cyfra jedności jest równa 3 lub 8.
Dany jest prostokąt 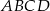 . Okręgi o średnicach
. Okręgi o średnicach 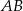 i
i 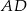 przecinają się w punktach
przecinają się w punktach 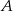 i
i 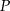 .
.
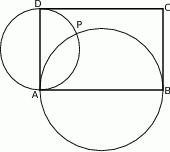
Wykaż, że punkty 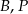 i
i 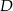 leżą na jednej prostej.
leżą na jednej prostej.
Na rysunku przedstawiono wykres funkcji 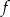 .
.
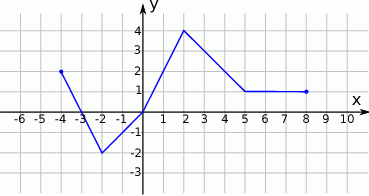
Odczytaj z wykresu i zapisz:
- zbiór wartości funkcji
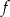 ,
, - przedział maksymalnej długości, w którym funkcja
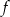 jest rosnąca.
jest rosnąca.
Oblicz wysokość trapezu o podstawach długości 18 i 14 oraz ramionach długości 3.
Wykaż, że liczba 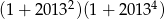 jest dzielnikiem liczby
jest dzielnikiem liczby
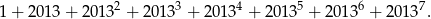
W układzie współrzędnych na płaszczyźnie punkty 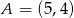 i
i 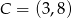 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 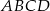 . Wyznacz równanie prostej
. Wyznacz równanie prostej 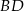 .
.
Ze zbioru liczb trzycyfrowych, które nie mają dwóch takich samych cyfr losujemy jedną liczbę. Jakie jest prawdopodobieństwo otrzymania liczby, której iloczyn cyfr jest liczbą niezerową podzielną przez 7?
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 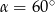 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
Zosia przez 30 dni kwietnia wrzucała do skarbonki pieniądze, przy czym każdego kolejnego dnia wrzucała o 2 zł więcej niż w dniu poprzednim. Wiedząc, że średnio wrzucała 33 zł złotych dziennie, oblicz ile pieniędzy wrzuciła do skarbonki 8 kwietnia.

