/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom rozszerzony 3 marca 2016 Czas pracy: 180 minut
Zadania zamknięte
Funkcja 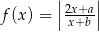 jest funkcją malejącą w przedziale
jest funkcją malejącą w przedziale 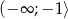 oraz
oraz 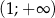 , rosnącą w przedziale
, rosnącą w przedziale 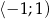 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 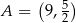 . Zatem wzór funkcji
. Zatem wzór funkcji 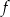 ma postać
ma postać
A) 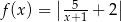 B)
B) 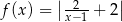 C)
C) 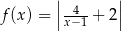 D)
D) 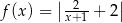
Liczb naturalnych siedmiocyfrowych, w zapisie których występuje dokładnie raz cyfra 7, dokładnie dwa razy cyfra 4, nie występuje cyfra zero, a pozostałe cyfry są między sobą różne jest
A) 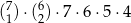 B)
B) 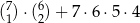 C)
C) 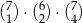 D)
D) 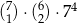
Ciąg 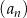 określony jest wzorem rekurencyjnym
określony jest wzorem rekurencyjnym 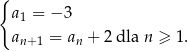 Wówczas wzór ogólny ciągu
Wówczas wzór ogólny ciągu 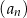 ma postać
ma postać
A) 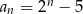 B)
B) 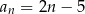 C)
C) 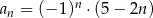 D)
D) 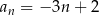
Zbiorem rozwiązań nierówności 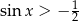 dla
dla 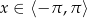 jest
jest
A) 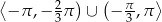 B)
B) 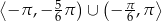
C) 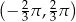 D)
D) 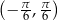
Granica 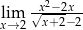 równa jest
równa jest
A) 0 B) 1 C) 8 D) 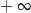
Zadania otwarte
Z pojemnika zawierającego 10 kul białych i 6 czarnych losujemy jedną kulę i wkładamy zamiast niej jedną kulę czarną. Oblicz prawdopodobieństwo tego, że jeżeli teraz wylosujemy z pojemnika dwie kule, to obie wylosowane kule będą białe. Zakoduj trzy pierwsze cyfry po przecinku otrzymanego rozwiązania.
W ciągu arytmetycznym suma  początkowych wyrazów o numerach parzystych jest równa
początkowych wyrazów o numerach parzystych jest równa 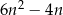 . Oblicz sumę
. Oblicz sumę  początkowych wyrazów o numerach nieparzystych.
początkowych wyrazów o numerach nieparzystych.
Wykaż, że jeżeli 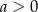 i
i 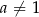 ,
, 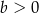 i
i 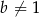 , to
, to 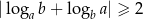 .
.
Na czworokącie 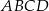 można opisać okrąg. Długości boków tego czworokąta są równe
można opisać okrąg. Długości boków tego czworokąta są równe 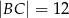 ,
, 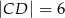 ,
, 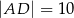 , a kąt
, a kąt 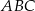 ma miarę
ma miarę 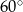 . Oblicz długość promienia okręgu opisanego na czworokącie
. Oblicz długość promienia okręgu opisanego na czworokącie 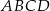 .
.
Funkcje 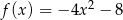 ,
, 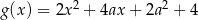 i
i 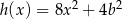 mają tę własność, że dla każdej liczby rzeczywistej
mają tę własność, że dla każdej liczby rzeczywistej  , wartości funkcji
, wartości funkcji 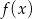 ,
, 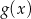 i
i 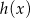 tworzą w pewnej kolejności trzywyrazowy ciąg geometryczny. Oblicz iloraz tego ciągu.
tworzą w pewnej kolejności trzywyrazowy ciąg geometryczny. Oblicz iloraz tego ciągu.
Rozwiąż nierówność, której lewa strona jest sumą szeregu geometrycznego (wszystkie składniki szeregu są różne od zera)
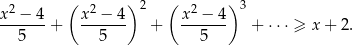
Udowodnij, że jeżeli liczba 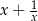 jest liczbą całkowitą, to liczba
jest liczbą całkowitą, to liczba 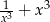 jest też liczbą całkowitą.
jest też liczbą całkowitą.
Rozwiąż równanie 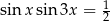 .
.
Długości krawędzi podstawy prostopadłościanu są równe 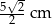 , a krawędź boczna ma długość 2 cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem
, a krawędź boczna ma długość 2 cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 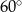 . Sporządź rysunek i zaznacz na nim przekrój oraz kąt jego nachylenia do płaszczyzny podstawy.
. Sporządź rysunek i zaznacz na nim przekrój oraz kąt jego nachylenia do płaszczyzny podstawy.
Wszystkie wierzchołki trapezu 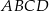 (
(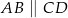 i
i 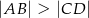 ) leżą na paraboli o równaniu
) leżą na paraboli o równaniu 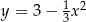 . Wierzchołki
. Wierzchołki 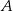 i
i 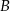 są punktami przecięcia tej paraboli z osią
są punktami przecięcia tej paraboli z osią 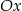 . Oblicz współrzędne wierzchołka trapezu o obu współrzędnych dodatnich, dla którego pole trapezu jest równe
. Oblicz współrzędne wierzchołka trapezu o obu współrzędnych dodatnich, dla którego pole trapezu jest równe 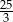 .
.
Liczby 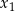 i
i 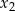 są wszystkimi pierwiastkami rzeczywistymi równania
są wszystkimi pierwiastkami rzeczywistymi równania 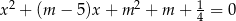 , przy czym zakładamy, że
, przy czym zakładamy, że 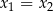 w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru
w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru 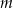 , wyrażenie
, wyrażenie 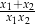 przyjmuje wartość najmniejszą. Oblicz tę wartość.
przyjmuje wartość najmniejszą. Oblicz tę wartość.

