/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 1 kwietnia 2023 Czas pracy: 180 minut
Wartość wyrażenia 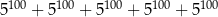 jest równa
jest równa
A) 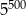 B)
B) 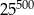 C)
C) 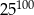 D)
D) 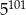
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 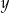 . Zatem 16% liczby
. Zatem 16% liczby 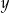 jest równe
jest równe
A) 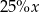 B)
B) 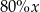 C)
C) 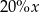 D)
D) 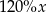
Tomek ma w skarbonce wyłącznie monety dwuzłotowe i pięciozłotowe. W sumie ma w skarbonce 351 zł. Gdyby dołożył do skarbonki 10 monet pięciozłotowych i dwie monety dwuzłotowe, to miałby w skarbonce dwa razy więcej monet dwuzłotowych, niż monet pięciozłotowych. Jeżeli oznaczymy przez  liczbę monet pięciozłotowych, a przez
liczbę monet pięciozłotowych, a przez 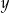 liczbę monet dwuzłotowych w skarbonce Tomka, to liczby
liczbę monet dwuzłotowych w skarbonce Tomka, to liczby  i
i 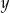 spełniają układ równań
spełniają układ równań
A) 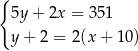 B)
B) 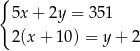
C) 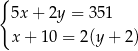 D)
D) 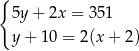
Jeżeli 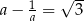 to liczba
to liczba 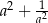 jest równa
jest równa
A) 9 B) 5 C) 1 D) 3
Na rysunku przedstawiono trapez 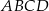 o podstawach
o podstawach 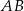 i
i 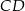 , w którym
, w którym 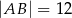 i
i 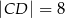 .
.
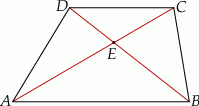
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Pola trójkątów utworzonych przez przekątne trapezu i jego boki spełniają równość
A) 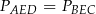 B)
B) 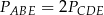 C)
C) 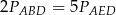
D) 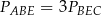 E)
E) 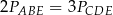 F)
F) 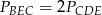
Dany jest wielomian 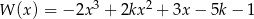 gdzie
gdzie 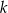 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 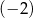 nie jest pierwiastkiem tego wielomianu. Zatem
nie jest pierwiastkiem tego wielomianu. Zatem
A) 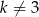 B)
B) 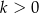 C)
C) 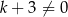 D)
D) 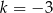
Wszystkich różnych liczb naturalnych czterocyfrowych, które są parzyste i podzielne przez 25, jest
A) 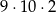 B)
B) 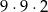 C)
C) 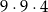 D)
D) 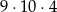
Informacja do zadań 8.1 i 8.2
W kartezjańskim układzie współrzędnych 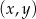 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 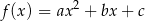 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 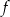 , ma współrzędne
, ma współrzędne 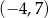 . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 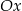 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 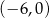 .
.
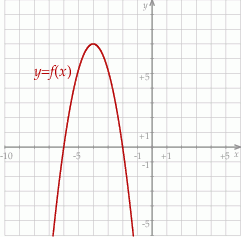
Wyznacz zbiór wszystkich wartości funkcji 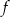 .
.
Wyznacz wzór funkcji kwadratowej 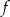 w postaci kanonicznej.
w postaci kanonicznej.
Firma przeprowadziła badania dotyczące wpływu zmiany dziennego kosztu produkcji 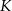 swojego produktu w zależności od liczby
swojego produktu w zależności od liczby 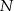 wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór
wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór
A) 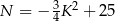 B)
B) 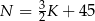
C) 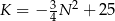 D)
D) 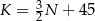
Ciąg 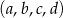 ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn
ma wszystkie wyrazy ujemne i jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 2. Oblicz iloczyn 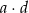 .
.
Informacja do zadań 11.1 i 11.2
Czas 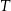 połowicznego rozpadu węgla
połowicznego rozpadu węgla 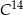 to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla
to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla 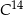 wynosi około
wynosi około 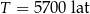 , a pozostała masa tego izotopu wyraża się wzorem
, a pozostała masa tego izotopu wyraża się wzorem
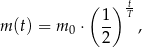
gdzie: 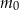 – masa izotopu węgla
– masa izotopu węgla 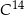 w trakcie życia organizmu
w trakcie życia organizmu 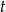 – czas jaki upłynął od czasu śmierci organizmu.
– czas jaki upłynął od czasu śmierci organizmu.
Jeżeli próbka materii organicznej została odkryta 39 900 lat po śmierci tego organizmu, a masa tego izotopu w trakcie życia organizmu była równa 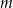 , to masa węgla
, to masa węgla 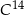 w tej próbce jest równa około
w tej próbce jest równa około
A) 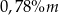 B)
B) 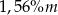 C)
C) 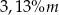 D)
D) 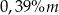
Pewien zespół naukowców w ramach prowadzonych badań archeologicznych odkrył szczątki żywego organizmu, w których masa izotopu węgla 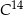 stanowi
stanowi 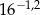 masy tego izotopu, jaka utrzymywała się podczas życia tego organizmu. Oblicz, ile lat mają odkryte szczątki organiczne.
masy tego izotopu, jaka utrzymywała się podczas życia tego organizmu. Oblicz, ile lat mają odkryte szczątki organiczne.
Równanie
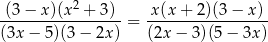
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Wiadomo, że 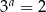 i
i 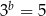 . Zatem liczba
. Zatem liczba 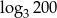 jest równa
jest równa
A) 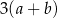 B)
B) 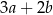 C)
C) 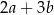 D)
D) 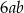
Na boku 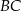 trójkąta równobocznego
trójkąta równobocznego 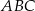 wybrano taki punkt
wybrano taki punkt 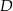 , że pole trójkąta
, że pole trójkąta 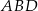 jest równe
jest równe 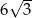 i jest dwa razy większe od pola trójkąta
i jest dwa razy większe od pola trójkąta 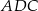 (zobacz rysunek).
(zobacz rysunek).
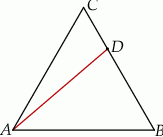
Oblicz długość odcinka 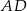 .
.
Pięciowyrazowy ciąg 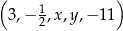 jest arytmetyczny. Liczby
jest arytmetyczny. Liczby  oraz
oraz 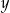 są równe
są równe
A) 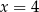 oraz
oraz 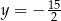 B)
B) 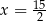 oraz
oraz 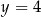
C) 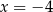 oraz
oraz 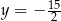 D)
D) 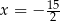 oraz
oraz 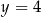
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 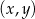 , dany jest okrąg
, dany jest okrąg 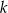 o środku
o środku 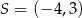 . Jednym z punktów leżących na tym okręgu jest
. Jednym z punktów leżących na tym okręgu jest 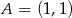 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Punkt 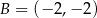 należy do okręgu należy do okręgu 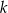 . . | P | F |
Promień okręgu 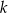 jest równy 29. jest równy 29. | P | F |
Punkt 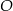 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 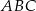 oraz
oraz 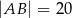 ,
, 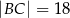 . Prosta
. Prosta 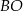 przecina bok
przecina bok 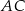 trójkąta
trójkąta 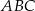 w punkcie
w punkcie 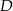 (zobacz rysunek).
(zobacz rysunek).
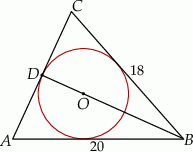
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 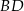 i i 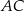 są prostopadłe. są prostopadłe. | P | F |
Stosunek pól trójkątów 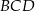 i i 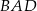 jest równy 0,9. jest równy 0,9. | P | F |
Końcami odcinka 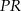 są punkty
są punkty 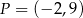 i
i 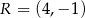 . Odległość punktu
. Odległość punktu 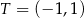 od środka odcinka
od środka odcinka 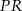 jest równa
jest równa
A) 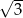 B)
B) 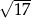 C)
C) 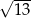 D)
D) 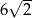
Ile rozwiązań ma równanie 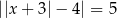 ?
?
A) 0 B) 2 C) 4 D) 6
Uzasadnij, że suma kwadratów trzech kolejnych liczb nieparzystych nigdy nie jest liczbą podzielną przez 3.
Informacja do zadań 21.1 i 21.2
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 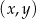 , dana jest prosta
, dana jest prosta 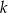 o równaniu
o równaniu 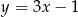 .
.
Jedną z prostych równoległych do prostej 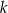 jest prosta o równaniu
jest prosta o równaniu
A) 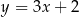 B)
B) 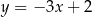 C)
C) 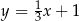 D)
D) 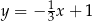
Jedną z prostych prostopadłych do prostej 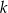 jest prosta o równaniu
jest prosta o równaniu
A) 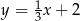 B)
B) 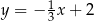 C)
C) 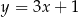 D)
D) 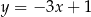
Dany jest sześcian 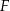 o krawędzi długości
o krawędzi długości  i objętości
i objętości 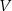 oraz sześcian
oraz sześcian 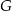 o krawędzi długości
o krawędzi długości 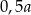 . Objętość sześcianu
. Objętość sześcianu 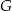 jest równa
jest równa
A) 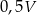 B)
B) 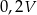 C)
C) 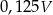 D)
D) 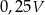
Kąt  jest ostry oraz
jest ostry oraz 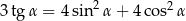 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 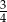 B)
B) 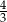 C)
C) 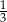 D) 3
D) 3
Wysokości 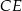 i
i 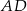 trójkąta równoramiennego
trójkąta równoramiennego 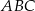 przecinają się w punkcie
przecinają się w punkcie 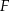 . Podstawa trójkąta
. Podstawa trójkąta 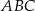 ma długość 13, a jego obwód jest równy 65.
ma długość 13, a jego obwód jest równy 65.
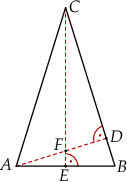
Stosunek pola trójkąta 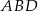 do pola trójkąta
do pola trójkąta 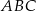 jest równy
jest równy
A)  B)
B) 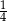 C)
C) 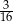 D)
D) 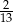
Dany jest ciąg 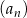 określony wzorem
określony wzorem 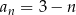 dla każdej liczby naturalnej
dla każdej liczby naturalnej 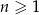 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A, B albo C oraz jej uzasadnienie 1, 2 albo 3.
Ciąg 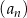 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 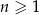
1) 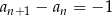 , , | 2) 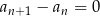 , , | 3) 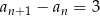 , , |
Punkty 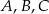 i
i 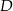 leżą na okręgu o środku
leżą na okręgu o środku 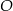 . Punkt
. Punkt 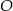 leży na odcinku
leży na odcinku 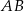 oraz
oraz 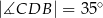 ,
, 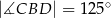 .
.
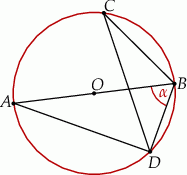
Miara kąta 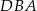 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A)  B)
B) 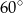 C)
C) 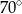 D)
D) 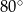
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania parzystej sumy oczek jest równe
A) 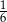 B)
B) 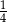 C)
C) 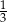 D)
D) 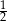
Środki ścian czworościanu foremnego 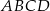 są wierzchołkami mniejszego czworościanu foremnego
są wierzchołkami mniejszego czworościanu foremnego 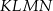 .
.
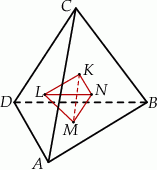
Stosunek objętości czworościanu 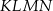 do objętości czworościanu
do objętości czworościanu 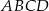 jest równy
jest równy
A) 8 : 27 B) 1 : 8 C) 1 : 64 D) 1 : 27
W eksperymencie badano kiełkowanie nasion w pięciu donicach. Na koniec eksperymentu policzono wykiełkowane nasiona w każdej z donic:
– w I donicy – 113 nasiona
– w II donicy – 141 nasion
– w III donicy – 99 nasion
– w IV donicy – 127 nasion
– w V donicy – 120 nasion.
Oblicz odchylenie standardowe liczby wykiełkowanych nasion.
Zakład ślusarski produkuje ozdobne kwietniki. Na podstawie analizy rzeczywistych wpływów i wydatków stwierdzono, że przychód 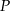 (w złotych) z tygodniowej sprzedaży
(w złotych) z tygodniowej sprzedaży  kwietników można opisać funkcją
kwietników można opisać funkcją
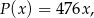
a koszt 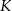 (w złotych) produkcji
(w złotych) produkcji  kwietników w ciągu jednego tygodnia można określić funkcją
kwietników w ciągu jednego tygodnia można określić funkcją
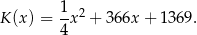
Tygodniowo w zakładzie można wyprodukować co najwyżej 250 kwietników. Oblicz, ile tygodniowo kwietników należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk.
Informacja do zadań 31.1 i 31.2
Firma 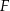 zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy 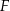 , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
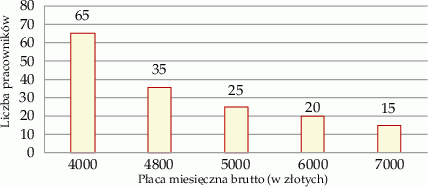
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Mediana miesięcznej płacy pracowników firmy  jest równa 4800 zł. jest równa 4800 zł. | P | F |
| Ponad 78% pracowników tej firmy zarabia nie więcej niż 5000 zł brutto. | P | F |
Średnia miesięczna płaca brutto w firmie 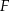 jest równa
jest równa
A) 4 862,5 zł B) 4 800,00 zł C) 5 360,00 zł D) 4 593,75 zł

