/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 9 marca 2018 Czas pracy: 170 minut
Zadania zamknięte
Narty w styczniu kosztowały 640 zł. W lutym obniżono ich cenę o 25%, a w marcu jeszcze o 10%. Cena nart po drugiej obniżce jest równa:
A) 416 zł B) 432 zł C) 605 zł D) 553,50 zł
Wykres funkcji liniowej 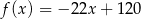 przechodzi przez ćwiartki układu współrzędnych:
przechodzi przez ćwiartki układu współrzędnych:
A) I, II, III B) I, II, IV C) I, III, IV D) II, III, IV
Funkcja, której wykres przedstawiono na rysunku, jest rosnąca w przedziałach
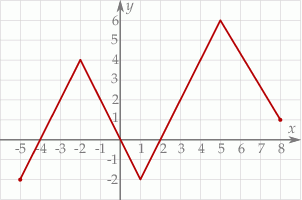
A) 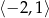 oraz
oraz 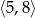 B)
B) 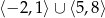 C)
C) 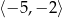 oraz
oraz 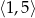 D)
D) 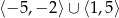
Ciąg 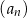 jest określony wzorem
jest określony wzorem 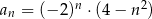 , dla
, dla 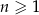 . Wtedy
. Wtedy
A) 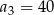 B)
B) 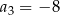 C)
C) 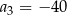 D)
D) 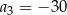
Cosinus kąta ostrego jest równy 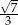 . Tangens tego kąta jest równy
. Tangens tego kąta jest równy
A) 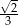 B)
B) 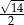 C)
C) 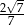 D)
D) 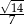
Funkcja kwadratowa, której fragment wykresu przedstawiono na rysunku, ma wzór
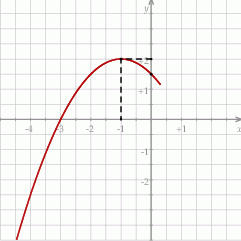
A) 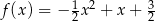 B)
B) 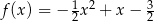
C) 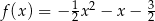 D)
D) 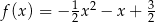
Wartość wyrażenia 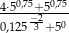 jest równa
jest równa
A) 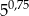 B)
B) 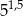 C)
C) 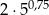 D)
D) 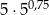
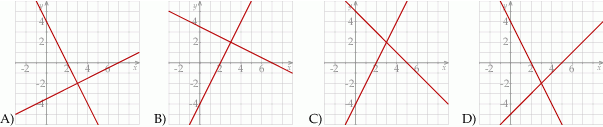
Ilustracja graficzna układu równań 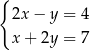 jest przedstawiona na rysunku:
jest przedstawiona na rysunku:
Iloczyn wszystkich rozwiązań równania 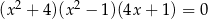 jest równy
jest równy
A) 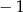 B)
B) 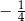 C)
C) 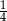 D) 1
D) 1
Kasia w pierwszym semestrze otrzymała następujące oceny z matematyki: z prac klasowych 3, 4, 4, 2, z kartkówek 5, 4, 4, 3, 5, z zadań domowych 3, 4, 5. Oceny z prac klasowych mają wagę 5, z kartkówek 3, z zadania domowego 2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Kasi w pierwszym semestrze jest równa
A) 3,71 B) 4,6 C) 13,7 D) 11,41
Jaką miarę ma kąt wpisany oparty na 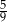 łuku okręgu?
łuku okręgu?
A) 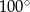 B)
B) 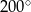 C)
C) 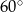 D)
D) 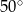
Proste o równaniach 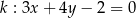 i
i 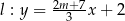 są równoległe, gdy
są równoległe, gdy
A) 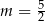 B)
B) 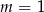 C)
C) 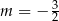 D)
D) 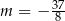
Liczba 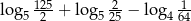 jest równa
jest równa
A) 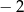 B) 1 C) 4 D) 3
B) 1 C) 4 D) 3
Obrazem odcinka 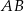 o końcach w punktach
o końcach w punktach 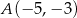 ,
, 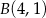 w symetrii względem osi
w symetrii względem osi 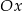 , jest odcinek
, jest odcinek 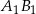 o końcach w punktach
o końcach w punktach
A) 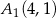 ,
, 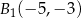 B)
B) 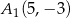 ,
, 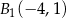
C) 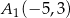 ,
, 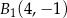 D)
D) 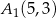 ,
, 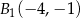
Wartość wyrażenia 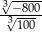 jest równa
jest równa
A) 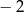 B)
B) 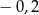 C) 2 D) 0,2
C) 2 D) 0,2
Wszystkimi rozwiązaniami równania wymiernego 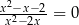 są
są
A) 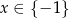 B)
B) 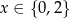 C)
C) 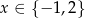 D)
D) 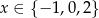
Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem 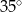 . Miara kąta rozwarcia stożka jest równa
. Miara kąta rozwarcia stożka jest równa
A) 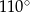 B)
B) 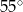 C)
C) 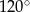 D)
D) 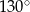
Funkcja liniowa przyjmuje wartości dodatnie dla 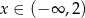 , a jej wykres przecina oś
, a jej wykres przecina oś 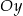 w punkcie
w punkcie 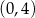 . Zatem jej wzór ma postać
. Zatem jej wzór ma postać
A) 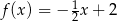 B)
B) 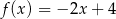 C)
C) 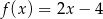 D)
D) 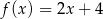
W ciągu arytmetycznym 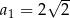 i
i 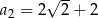 . Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
. Suma wyrazów od dziesiątego do czterdziestego włącznie jest równa
A) 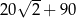 B)
B) 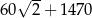 C)
C) 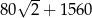 D)
D) 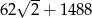
Punkt 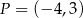 leży na końcowym ramieniu kąta
leży na końcowym ramieniu kąta  . Cosinus kąta
. Cosinus kąta  jest równy
jest równy
A)  B)
B) 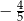 C)
C)  D)
D) 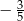
Liczb naturalnych sześciocyfrowych podzielnych przez 5, których cyfra setek należy do zbioru 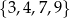 i wszystkie cyfry są różne jest
i wszystkie cyfry są różne jest
A) 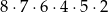 B)
B) 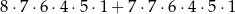
C) 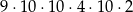 D)
D) 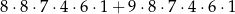
Wykres funkcji 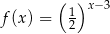 przedstawiony jest na rysunku
przedstawiony jest na rysunku
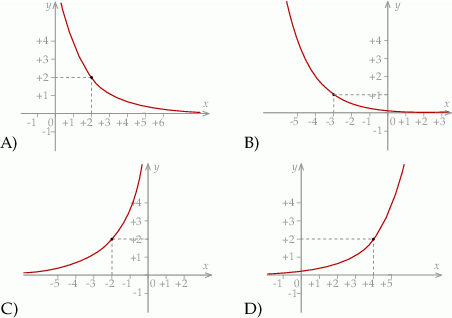
Liczba 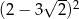 jest równa
jest równa
A) 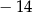 B) 22 C)
B) 22 C) 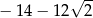 D)
D) 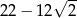
Miara kąta między bokiem 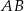 równoległoboku
równoległoboku 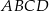 , a przekątną
, a przekątną 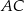 jest równa
jest równa 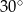 . Długość przekątnej
. Długość przekątnej 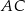 jest równa 5, a długość boku
jest równa 5, a długość boku 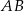 wynosi 4, zatem pole równoległoboku jest równe
wynosi 4, zatem pole równoległoboku jest równe
A) 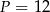 B)
B) 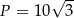 C)
C) 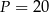 D)
D) 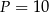
Największą wartością funkcji kwadratowej 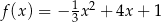 w przedziale
w przedziale 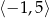 jest
jest
A) 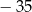 B)
B) 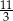 C)
C) 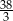 D) 13
D) 13
Zadania otwarte
Rozwiąż nierówność 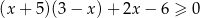 .
.
W trójkącie równobocznym 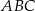 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 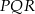 . Wykaż, że stosunek pola trójkąta
. Wykaż, że stosunek pola trójkąta 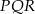 do pola trójkąta
do pola trójkąta 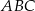 jest równy
jest równy 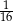 .
.
Wyznacz wzór ogólny ciągu geometrycznego wiedząc, że 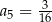 oraz
oraz 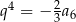 .
.
Udowodnij, że jeżeli przy dzieleniu przez 5 liczba całkowita  daje resztę 2, a liczba całkowita
daje resztę 2, a liczba całkowita 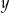 daje resztę 3, to iloczyn liczb
daje resztę 3, to iloczyn liczb  i
i 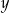 przy dzieleniu przez 5 daje resztę 1.
przy dzieleniu przez 5 daje resztę 1.
Wyznacz równanie symetralnej odcinka 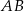 , gdzie
, gdzie 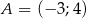 i
i 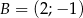 .
.
Ze zbioru liczb 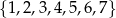 losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 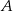 polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
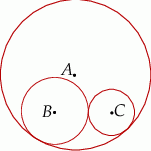
Dane dwa okręgi o środkach 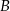 i
i 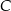 są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie
są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie 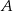 . Wiedząc, że
. Wiedząc, że 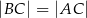 oraz promień okręgu o środku
oraz promień okręgu o środku 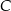 ma długość
ma długość 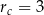 oblicz długość odcinka
oblicz długość odcinka 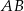 .
.
Czworokąt 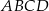 jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki
jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki 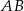 i
i 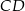 , przy czym
, przy czym 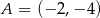 ,
, 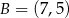 i
i 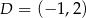 , oblicz pole oraz obwód trapezu.
, oblicz pole oraz obwód trapezu.
Podstawą ostrosłupa jest prostokąt, którego stosunek długości boków wynosi 2:3. Pole podstawy ostrosłupa jest równe 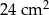 . Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem
. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 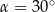 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.

