/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 27 marca 2021 Czas pracy: 170 minut
Zadania zamknięte
Wiadomo, że 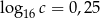 . Zatem liczba
. Zatem liczba  jest
jest
A) niewymierna B) wymierna C) większa od 2 D) mniejsza od 1
Liczba 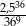 jest równa
jest równa
A) 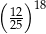 B)
B) 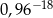 C)
C) 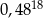 D)
D) 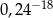
Stężenie roztworu początkowo wzrosło o 20%, a po 15 minutach wzrosło o dalsze 30%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 56% C) 50% D) 60%
Najmniejszą liczbą całkowitą spełniającą nierówność 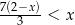 jest liczba
jest liczba
A) 1 B) 2 C) 3 D) 4
Najmniejsza wartość wyrażenia 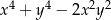 dla
dla 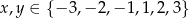 jest równa
jest równa
A) 0 B) 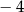 C) 2 D)
C) 2 D) 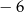
Suma wszystkich rozwiązań równania 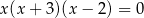 jest równa
jest równa
A) 0 B) 1 C) 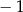 D) 6
D) 6
Liczba naturalna  przy dzieleniu przez 8 daje resztę 6. Liczbę
przy dzieleniu przez 8 daje resztę 6. Liczbę  można więc zapisać w postaci
można więc zapisać w postaci 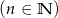
A) 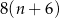 B)
B) 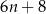 C)
C) 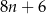 D)
D) 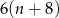
Zbiorem wartości funkcji kwadratowej 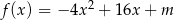 jest przedział
jest przedział 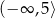 . Wtedy
. Wtedy
A) 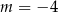 B)
B) 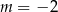 C)
C) 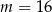 D)
D) 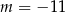
Jeżeli  jest liczbą dodatnią i
jest liczbą dodatnią i 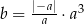 , to
, to
A) 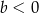 B)
B) 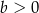 C)
C) 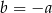 D)
D) 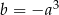
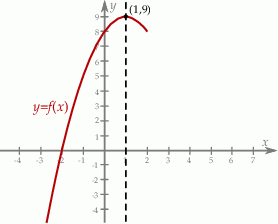
Na podstawie fragmentu wykresu funkcji kwadratowej 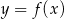 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
A) Miejscami zerowymi funkcji są liczby: 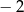 oraz 4.
oraz 4.
B) Funkcja jest rosnąca w przedziale 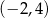 .
.
C) Funkcja przyjmuje wartości większe od zera dla 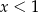 .
.
D) Zbiorem wartości funkcji jest przedział 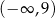 .
.
Do zbioru rozwiązań nierówności 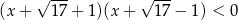 należy liczba
należy liczba
A) 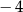 B)
B) 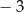 C)
C) 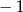 D) 3
D) 3
Funkcja 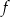 jest określona wzorem
jest określona wzorem 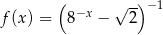 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Liczba
. Liczba 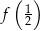 jest równa
jest równa
A) 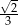 B)
B) 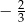 C)
C) 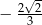 D)
D) 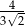
Do okręgu o środku w punkcie 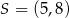 należy punkt
należy punkt 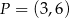 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 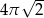 B)
B) 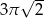 C)
C) 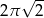 D)
D) 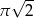
Dany jest nieskończony rosnący ciąg arytmetyczny 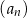 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 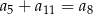 B)
B) 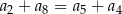 C)
C) 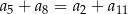 D)
D) 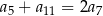
Liczby 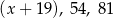 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
A) 62 B) 36 C) 35 D) 17
Punkt 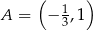 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 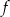 określonej wzorem
określonej wzorem 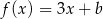 . Wynika stąd, że
. Wynika stąd, że
A) 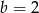 B)
B) 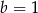 C)
C) 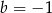 D)
D) 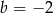
Wiadomo, że sinus kąta  trójkąta przedstawionego na rysunku jest równy
trójkąta przedstawionego na rysunku jest równy 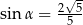 .
.
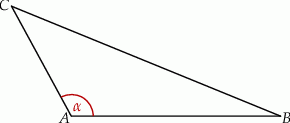
Wtedy
A) 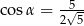 B)
B) 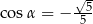 C)
C) 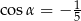 D)
D) 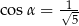
Punkt 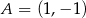 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 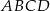 , którego bok
, którego bok 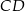 zawiera się w prostej
zawiera się w prostej 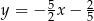 . Podstawa
. Podstawa 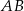 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 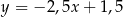 B)
B) 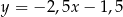 C)
C) 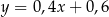 D)
D) 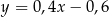
Dany jest okrąg o środku w punkcie 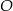 . Prosta
. Prosta 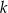 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 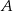 .
.
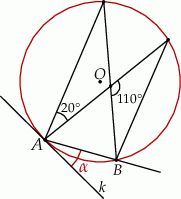
Miara kąta  jest równa
jest równa
A) 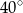 B)
B) 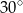 C)
C) 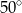 D)
D) 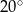
Punkt 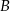 jest obrazem punktu
jest obrazem punktu 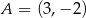 w symetrii względem początku układu współrzędnych, a punkt
w symetrii względem początku układu współrzędnych, a punkt 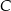 jest obrazem punktu
jest obrazem punktu 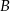 w symetrii względem punktu
w symetrii względem punktu 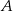 . Długość odcinka
. Długość odcinka 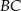 jest równa
jest równa
A) 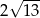 B)
B) 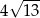 C)
C) 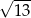 D)
D) 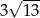
Wielkości  i
i 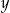 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 | 3 |  | 2 |
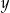 | 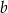 | 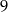 | 36 |
Stąd wynika, że
A) 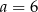 ,
, 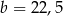 B)
B) 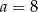 ,
, 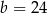 C)
C) 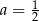 ,
, 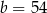 D)
D) 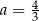 ,
, 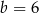
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 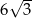 B)
B) 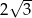 C)
C) 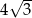 D)
D) 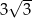
Prostą prostopadłą do prostej o równaniu 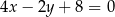 jest prosta o równaniu
jest prosta o równaniu
A) 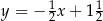 B)
B) 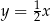 C)
C) 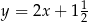 D)
D) 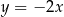
Przekątna sześcianu ma długość 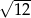 . Pole powierzchni tego sześcianu jest równe
. Pole powierzchni tego sześcianu jest równe
A) 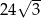 B) 24 C) 12 D)
B) 24 C) 12 D) 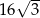
Ostrosłup rozcięto płaszczyzną równoległą do płaszczyzny podstawy na dwie bryły, przy czym jedna z nich ma o 12 krawędzi więcej od drugiej. Ile wierzchołków miał ostrosłup przed rozcięciem?
A) 12 B) 13 C) 26 D) 24
Losujemy jeden bok i jeden wierzchołek pięciokąta foremnego. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowany wierzchołek jest końcem wylosowanego odcinka jest równe
A) 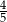 B)
B) 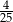 C)
C) 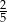 D)
D) 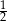
Liczba sześcianów liczb całkowitych w zbiorze kolejnych liczb naturalnych
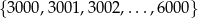
jest równa
A) 3 B) 4 C) 5 D) 8
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 3 | 7 | 6 | 9 | 2 | 0 |
Średnia ocen w tej klasie jest równa
A) 3 B) 3,5 C) 4 D) 5
Zadania otwarte
Wyznacz wszystkie liczby rzeczywiste  , które spełniają warunek:
, które spełniają warunek: 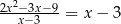 .
.
Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 5.
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
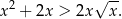
Dany jest trzywyrazowy ciąg 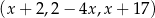 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Trójkąty prostokątne równoramienne 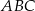 i
i 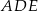 są położone tak, jak na poniższym rysunku.
są położone tak, jak na poniższym rysunku.
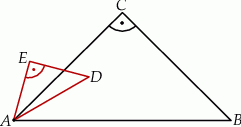
Wykaż, że 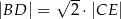 .
.
Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, która zawiera krawędź podstawy oraz przechodzi przez środek przeciwległej krawędzi bocznej (zobacz rysunek).
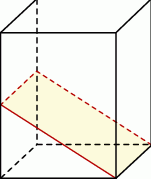
Oblicz jaki jest stosunek objętości dwóch brył na jakie został podzielony ten graniastosłup.
Dany jest kwadrat 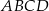 , w którym
, w którym 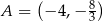 . Przekątna
. Przekątna 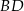 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 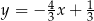 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 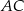 i
i 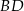 oraz pole kwadratu
oraz pole kwadratu 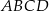 .
.

