/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom podstawowy 14 grudnia 2022 Czas pracy: 180 minut
Liczba 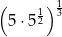 jest równa
jest równa
A) 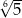 B)
B) 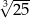 C)
C) 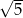 D)
D) 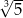
Pan Nowak kupił obligacje Skarbu Państwa za 40 000 zł oprocentowane 7% w skali roku. Odsetki są naliczane i kapitalizowane co rok. Wartość obligacji kupionych przez pana Nowaka będzie po dwóch latach równa
A) 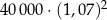 B)
B) 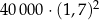 C)
C) 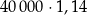 D)
D) 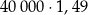
Właściciel sklepu kupił w hurtowni 50 par identycznych spodni po  zł za parę i 40 identycznych marynarek po
zł za parę i 40 identycznych marynarek po 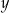 zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni
zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni  oraz cenę marynarki
oraz cenę marynarki 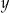 , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 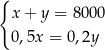 B)
B) 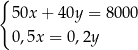 C)
C) 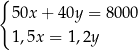 D)
D) 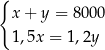
Liczby rzeczywiste  i
i 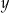 są dodatnie oraz
są dodatnie oraz 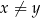 . Wyrażenie
. Wyrażenie 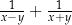 można przekształcić do postaci
można przekształcić do postaci
A) 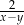 B)
B) 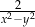 C)
C) 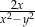 D)
D) 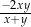
Wszystkich różnych liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym wszystkie cyfry są różne, jest
A) 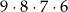 B)
B) 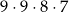 C)
C) 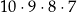 D)
D) 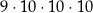
Funkcja 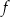 jest określona wzorem
jest określona wzorem 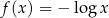 dla wszystkich liczb rzeczywistych dodatnich
dla wszystkich liczb rzeczywistych dodatnich  . Wartość funkcji
. Wartość funkcji 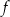 dla argumentu
dla argumentu 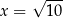 jest równa
jest równa
A) 2 B) 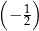 C)
C) 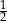 D)
D) 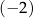
Informacja do zadań 7.1 i 7.2
W kartezjańskim układzie współrzędnych 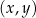 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 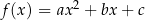 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 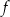 , ma współrzędne
, ma współrzędne 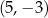 . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 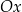 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 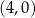 .
.
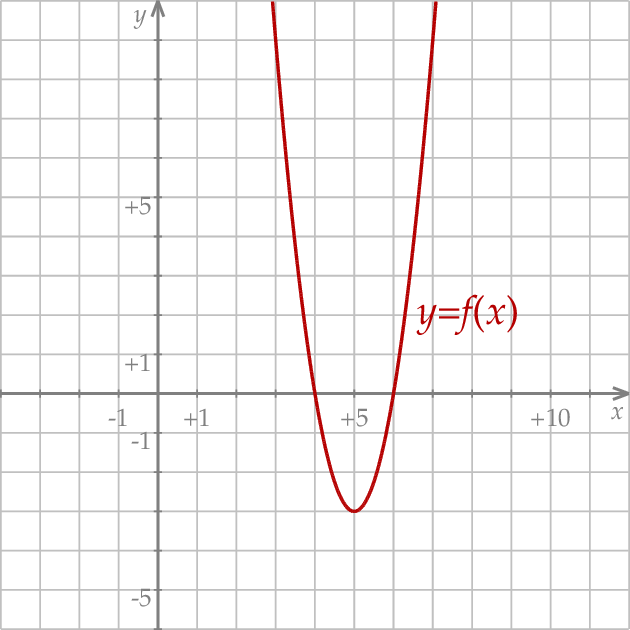
Wyznacz zbiór wszystkich wartości funkcji 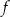 .
.
Wyznacz wzór funkcji kwadratowej 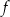 w postaci kanonicznej.
w postaci kanonicznej.
Dana jest nierówność kwadratowa
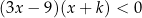
z niewiadomą  i parametrem
i parametrem 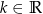 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 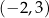 . Liczba
. Liczba 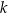 jest równa
jest równa
A) 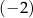 B) 2 C)
B) 2 C) 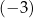 D) 3
D) 3
Dana jest funkcja kwadratowa 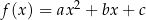 , gdzie
, gdzie 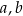 i
i  są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 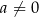 oraz
oraz 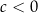 . Funkcja
. Funkcja 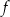 nie ma miejsc zerowych.
nie ma miejsc zerowych.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Wykres funkcji 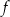 leży w całości
leży w całości
A) nad osią 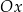 , , | B) pod osią 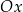 , , |
| ponieważ | |
| 1) | 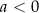 i i 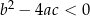 . . |
| 2) | 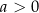 i i 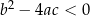 . . |
| 3) | 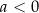 i i 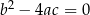 . . |
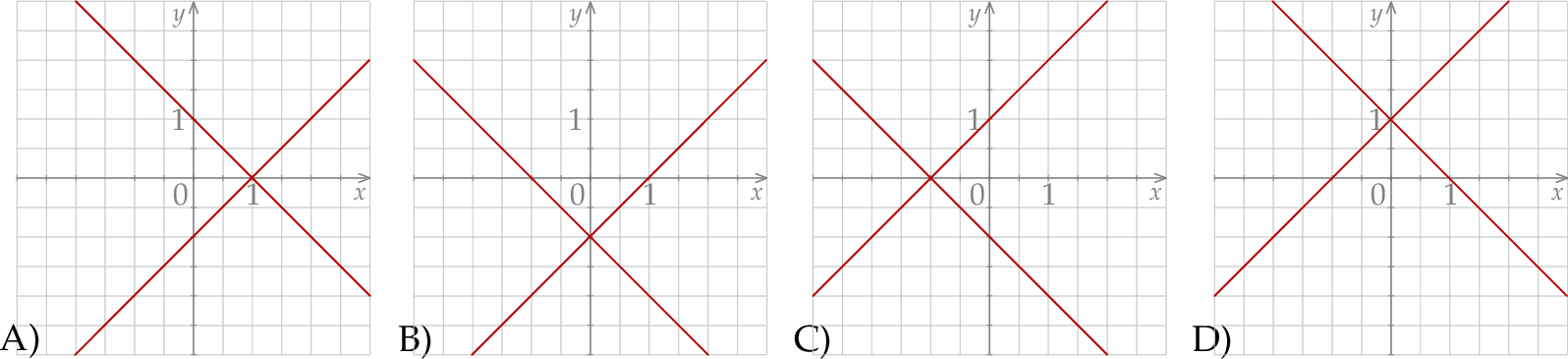
Dany jest układ równań
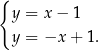
Na którym z rysunków przedstawiona jest interpretacja geometryczna tego układu równań?
Dany jest wielomian 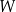 określony wzorem
określony wzorem 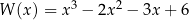 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 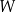 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 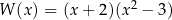 B)
B) 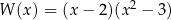
C) 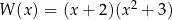 D)
D) 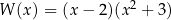
Równanie 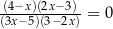 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Dana jest nierówność
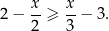
Największą liczbą całkowitą, która spełnia tę nierówność, jest
A) 6 B) 5 C) 7 D) 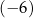
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 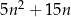 jest podzielna przez 10.
jest podzielna przez 10.
Dany jest ciąg 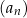 określony wzorem
określony wzorem 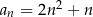 dla każdej liczby naturalnej
dla każdej liczby naturalnej 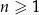 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ciąg 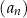 jest malejący. jest malejący. | P | F |
Ósmy wyraz ciągu 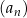 jest równy 136. jest równy 136. | P | F |
Pięciowyrazowy ciąg 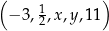 jest arytmetyczny. Liczby
jest arytmetyczny. Liczby  oraz
oraz 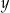 są równe
są równe
A) 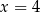 oraz
oraz 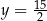 B)
B) 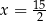 oraz
oraz 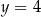
C) 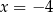 oraz
oraz 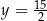 D)
D) 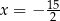 oraz
oraz 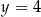
Dany jest ciąg geometryczny 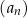 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 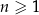 . W tym ciągu
. W tym ciągu 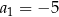 ,
, 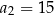 ,
, 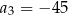 .
.
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór ogólny ciągu 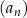 ma postać
ma postać
A) 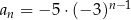 B)
B) 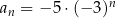
C) 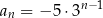 D)
D) 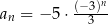
E) 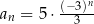 F)
F) 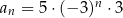
Kąt  jest ostry oraz
jest ostry oraz 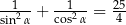 . Wartość wyrażenia
. Wartość wyrażenia 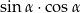 jest równa
jest równa
A)  B)
B)  C)
C) 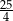 D)
D) 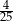
Punkty 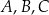 leżą na okręgu o środku
leżą na okręgu o środku 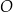 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 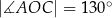 oraz
oraz 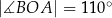 .
.
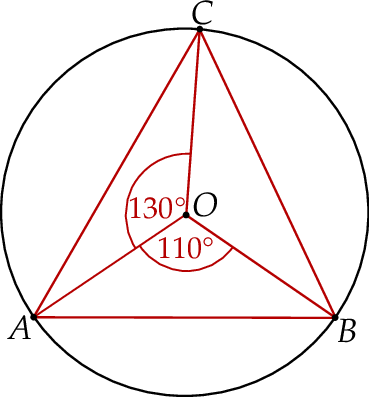
Miara kąta wewnętrznego 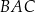 trójkąta
trójkąta 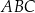 jest równa
jest równa
A) 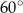 B)
B) 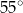 C)
C) 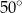 D)
D) 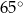
Do wyznaczenia trzech boków pewnego kąpieliska w kształcie prostokąta należy użyć liny o długości 200 m. Czwarty bok tego kąpieliska będzie pokrywał się z brzegiem plaży, który w tym miejscu jest linią prostą (zobacz rysunek).
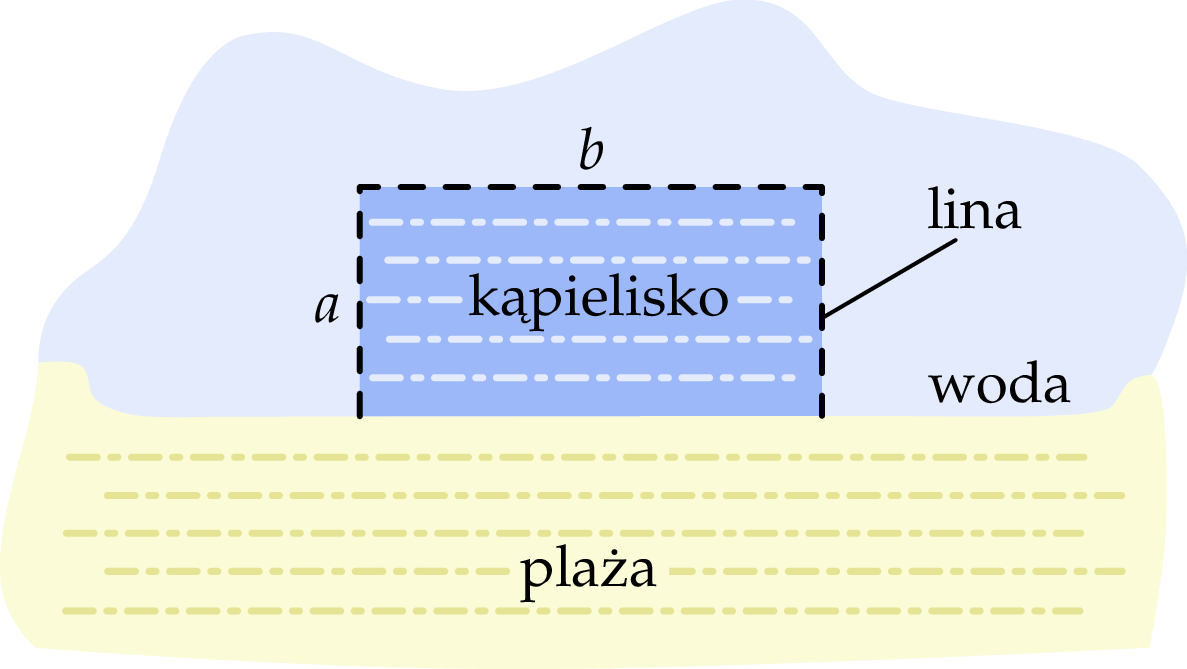
Oblicz wymiary  i
i 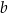 kąpieliska tak, aby jego powierzchnia była największa.
kąpieliska tak, aby jego powierzchnia była największa.
Dany jest kwadrat 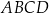 o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka  zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
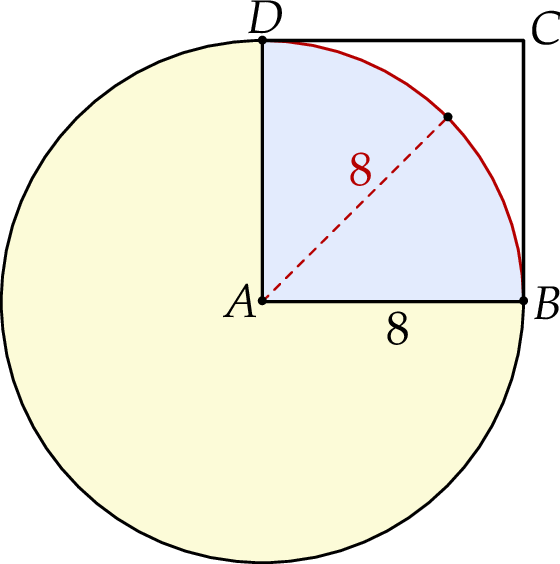
Pole powierzchni części wspólnej koła i kwadratu jest równe
A) 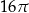 B)
B) 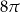 C)
C) 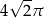 D)
D) 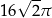
Odcinki 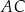 i
i 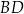 przecinają się w punkcie
przecinają się w punkcie 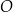 . Ponadto
. Ponadto 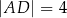 i
i 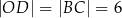 . Kąty
. Kąty 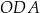 i
i 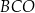 są proste (zobacz rysunek).
są proste (zobacz rysunek).

Długość odcinka 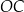 jest równa
jest równa
A) 9 B) 8 C) 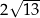 D)
D) 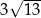
Przekątne równoległoboku 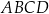 mają długości:
mają długości: 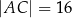 oraz
oraz 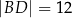 . Wierzchołki
. Wierzchołki 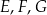 oraz
oraz 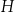 rombu
rombu 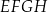 leżą na bokach równoległoboku
leżą na bokach równoległoboku 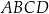 (zobacz rysunek). Boki tego rombu są równoległe do przekątnych równoległoboku.
(zobacz rysunek). Boki tego rombu są równoległe do przekątnych równoległoboku.
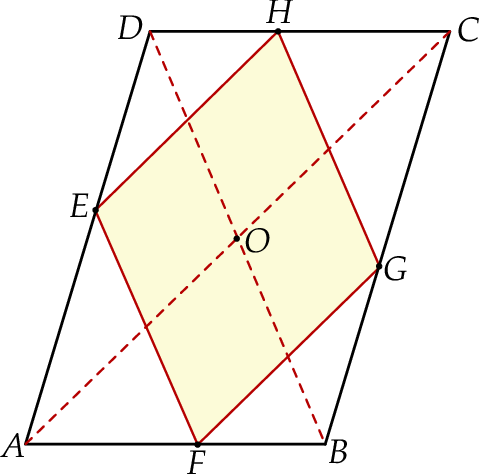
Oblicz długość boku rombu 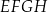 .
.
Dany jest trójkąt 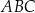 , w którym
, w którym 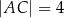 ,
, 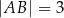 ,
, 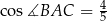 . Oblicz pole trójkąta
. Oblicz pole trójkąta 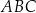 .
.
Informacja do zadań 25.1 i 25.2
Dany jest sześciokąt foremny 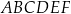 o polu równym
o polu równym 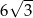 (zobacz rysunek).
(zobacz rysunek).

Pole trójkąta 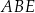 jest równe
jest równe
A) 6 B) 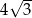 C)
C) 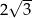 D) 4
D) 4
Długość odcinka 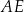 jest równa
jest równa
A) 2 B) 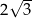 C)
C) 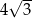 D) 4
D) 4
Dany jest trapez 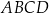 , w którym
, w którym 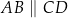 oraz przekątne
oraz przekątne 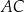 i
i 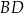 przecinają się w punkcie
przecinają się w punkcie 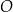 . Wysokość tego trapezu jest równa 12. Obwód trójkąta
. Wysokość tego trapezu jest równa 12. Obwód trójkąta 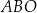 jest równy 39, a obwód trójkąta
jest równy 39, a obwód trójkąta 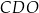 jest równy 13.
jest równy 13.
Wysokość trójkąta  poprowadzona z punktu
poprowadzona z punktu  jest równa
jest równa
A) 3 B) 4 C) 9 D) 6
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 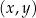 , dany jest okrąg
, dany jest okrąg  o równaniu
o równaniu
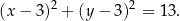
Okrąg  przecina oś
przecina oś 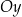 w punktach o współrzędnych
w punktach o współrzędnych
A) 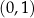 i
i 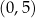 B)
B) 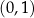 i
i 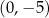
C) 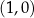 i
i 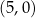 D)
D) 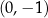 i
i 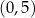
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 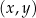 , dane są proste
, dane są proste 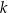 oraz
oraz 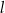 o równaniach
o równaniach
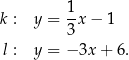
Proste 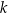 oraz
oraz 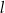
A) nie mają punktów wspólnych. B) są prostopadłe.
C) przecinają się w punkcie 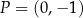 . D) pokrywają się.
. D) pokrywają się.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 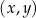 , dane są punkty
, dane są punkty 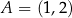 i
i 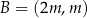 , gdzie
, gdzie 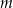 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 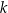 o równaniu
o równaniu 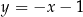 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 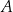 i
i 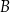 jest równoległa do prostej
jest równoległa do prostej 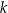 , gdy
, gdy
A) 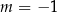 B)
B) 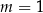 C)
C) 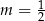 D)
D) 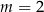
Informacja do zadań 30.1 i 30.2
Dany jest sześcian 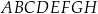 o krawędzi długości 9. Wierzchołki podstawy
o krawędzi długości 9. Wierzchołki podstawy 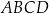 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 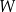 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy  . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny  .
.
Objętość 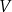 ostrosłupa
ostrosłupa 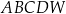 jest równa
jest równa
A) 243 B) 364,5 C) 489 D) 729
Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dany jest sześcian 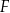 o krawędzi długości
o krawędzi długości  i objętości
i objętości 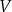 oraz sześcian
oraz sześcian 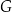 o krawędzi długości
o krawędzi długości 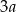 . Objętość sześcianu
. Objętość sześcianu 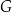 jest równa
jest równa
A) 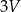 B)
B) 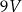 C)
C) 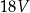 D)
D) 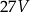
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest wygrywający, jest równe
A) 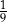 B)
B) 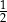 C)
C) 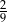 D)
D) 
W eksperymencie badano kiełkowanie nasion w pięciu donicach. Na koniec eksperymentu policzono wykiełkowane nasiona w każdej z donic:
– w I donicy – 133 nasiona
– w II donicy – 140 nasion
– w III donicy – 119 nasion
– w IV donicy – 147 nasion
– w V donicy – 161 nasion.
Odchylenie standardowe liczby wykiełkowanych nasion jest równe 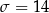 . Podaj numery donic, w których liczba wykiełkowanych nasion mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej.
. Podaj numery donic, w których liczba wykiełkowanych nasion mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej.

