/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 3 marca 2018 Czas pracy: 170 minut
Zadania zamknięte
Adam kupił 2 owoce mango po 3,40 zł każdy oraz 1,5 kg jabłek po 2,20 zł za kilogram. Obliczył, że za zakupy zapłaci w przybliżeniu 10 zł. Błąd względny tego przybliżenia wynosi:
A) 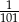 B) 0,1 C) 0,01 D)
B) 0,1 C) 0,01 D) 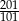
Liczba 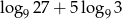 jest równa
jest równa
A) 2 B) 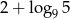 C) 4 D)
C) 4 D) 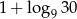
Liczba 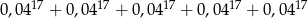 jest równa
jest równa
A) 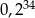 B)
B) 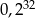 C)
C) 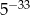 D)
D) 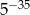
Liczba uczniów pewnej szkoły zmalała w stosunku do 1 września 2010 roku o 25% i obecenie jest równa 735. Ilu uczniów liczyła ta szkoła na początku roku szkolnego 2010/2011?
A) 551 B) 919 C) 980 D) 1050
Ile jest liczb całkowitych  spełniających nierówność
spełniających nierówność 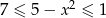 ?
?
A) nieskończenie wiele B) 0 C) 5 D) 1
Wartość wyrażenia 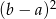 dla
dla 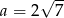 i
i 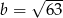 jest równa
jest równa
A) 49 B) 35 C) 7 D) 245
Zbiorem wartości funkcji kwadratowej 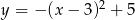 określonej dla
określonej dla 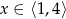 jest przedział
jest przedział
A) 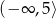 B)
B) 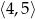 C)
C) 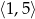 D)
D) 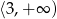
Równanie 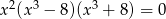 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Liczba 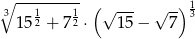 jest równa
jest równa
A) 2 B) 8 C) 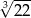 D)
D) 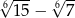
Liczba 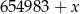 daje resztę 7 z dzielenia przez 9. Liczba
daje resztę 7 z dzielenia przez 9. Liczba  może być równa
może być równa
A) 2 B) 3 C) 7 D) 8
Funkcja kwadratowa 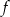 jest określona wzorem
jest określona wzorem 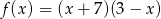 . Wierzchołek paraboli będącej wykresem funkcji
. Wierzchołek paraboli będącej wykresem funkcji 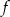 należy do prostej o równaniu
należy do prostej o równaniu
A) 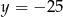 B)
B) 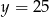 C)
C) 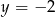 D)
D) 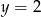
W ciągu arytmetycznym 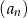 , określonym dla
, określonym dla 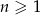 , dane są:
, dane są: 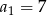 ,
, 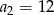 . Wtedy
. Wtedy
A) 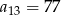 B)
B) 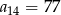 C)
C) 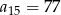 D)
D) 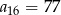
Dwa kolejne wyrazy ciągu geometrycznego 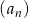 są równe 9 i 15. Wyrazem tego ciągu może być liczba
są równe 9 i 15. Wyrazem tego ciągu może być liczba
A) 6,25 B) 21 C) 24,5 D) 5,4
Jeżeli wiadomo, że  jest kątem rozwartym i
jest kątem rozwartym i 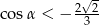 , to
, to 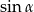 jest liczbą z przedziału
jest liczbą z przedziału
A) 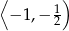 B)
B) 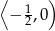 C)
C) 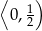 D)
D) 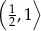
Na przyprostokątnych 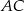 i
i 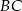 trójkąta prostokątnego
trójkąta prostokątnego 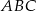 wybrano punkty
wybrano punkty 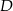 i
i 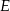 tak, że
tak, że 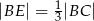 i
i 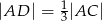 . Punkty
. Punkty 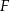 i
i 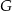 leżą na przeciwprostokątnej
leżą na przeciwprostokątnej 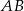 tak, że odcinki
tak, że odcinki 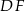 i
i 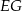 są do niej prostopadłe (zobacz rysunek). Pole trójkąta
są do niej prostopadłe (zobacz rysunek). Pole trójkąta 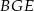 jest równe 1, a pole trójkąta
jest równe 1, a pole trójkąta 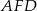 jest równe 4.
jest równe 4.
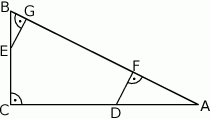
Zatem pole trójkąta 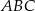 jest równe
jest równe
A) 40 B) 15 C) 45 D) 20
Przekątne trapezu 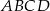 przecinają się w punkcie
przecinają się w punkcie 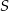 w ten sposób, że
w ten sposób, że 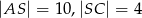 ,
, 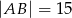 .
.
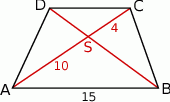
Długość odcinka  jest równa
jest równa
A) 4 B) 6 C) 8 D) 9
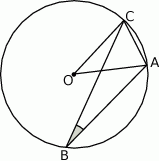
W okręgu o środku  dany jest kąt wpisany
dany jest kąt wpisany  o mierze
o mierze 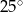 (patrz rysunek).
(patrz rysunek).
Miara kąta 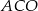 jest równa
jest równa
A) 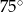 B)
B) 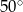 C)
C) 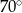 D)
D) 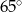
Punkty 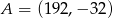 ,
, 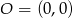 i
i 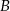 są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej
są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej 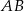 . Wskaż równanie prostej zawierającej przyprostokątną
. Wskaż równanie prostej zawierającej przyprostokątną 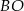 tego trójkąta.
tego trójkąta.
A) 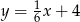 B)
B) 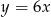 C)
C) 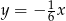 D)
D) 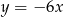
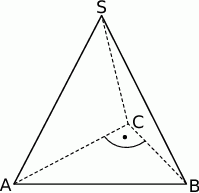
Na rysunku przedstawiono ostrosłup czworokątny 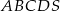 , którego podstawą jest kwadrat
, którego podstawą jest kwadrat 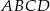 , i w którym krawędź
, i w którym krawędź 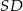 jest prostopadła do płaszczyzny podstawy (patrz rysunek).
jest prostopadła do płaszczyzny podstawy (patrz rysunek).
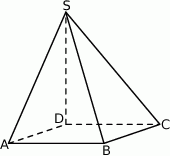
Które trzy punkty nie są wierzchołkami trójkąta prostokątnego?
A) 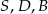 B)
B) 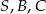 C)
C) 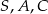 D)
D) 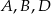
Dany jest okrąg o środku 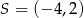 i promieniu
i promieniu 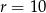 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 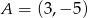 B)
B) 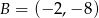 C)
C) 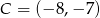 D)
D) 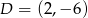
Dany jest stożek o wysokości 6 i tworzącej 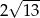 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 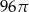 B)
B) 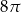 C)
C) 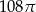 D)
D) 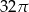
Pole trójkąta prostokątnego 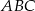 , przedstawionego na rysunku, jest równe
, przedstawionego na rysunku, jest równe
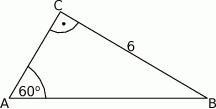
A) 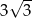 B)
B) 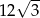 C)
C) 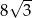 D)
D) 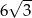
Przekątna ściany sześcianu ma długość 6. Przekątna tego sześcianu ma długość
A) 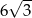 B)
B) 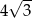 C)
C) 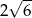 D)
D) 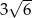
Po usunięciu jednej liczby z listy danych: 3, 2, 5, 4, 1, 5, 2, 4, 1, 5 średnia arytmetyczna zmniejszyła się o 0,2. Którą liczbę usunięto z listy?
A) 2 B) 3 C) 4 D) 5
W pudełku jest 5 kul czerwonych i  kul żółtych. Prawdopodobieństwo wylosowania kuli żółtej jest równe
kul żółtych. Prawdopodobieństwo wylosowania kuli żółtej jest równe  , gdy
, gdy
A) 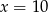 B)
B) 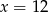 C)
C) 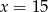 D)
D) 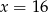
Zadania otwarte
Rozwiąż nierówność 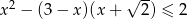 .
.
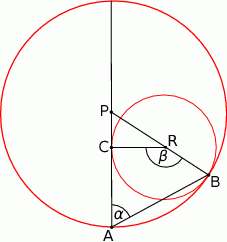
Dane są dwa okręgi o środkach w punktach 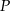 i
i 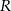 , styczne wewnętrznie w punkcie
, styczne wewnętrznie w punkcie 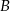 . Prosta
. Prosta 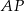 jest styczna do mniejszego okręgu w punkcie
jest styczna do mniejszego okręgu w punkcie 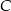 oraz
oraz 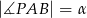 i
i 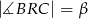 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 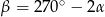 .
.
Udowodnij, że dla dowolnej ujemnej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
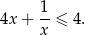
Suma czterdziestu początkowych wyrazów ciągu arytmetycznego 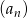 , określonego dla
, określonego dla 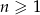 , jest równa 40. Ponadto
, jest równa 40. Ponadto 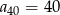 . Oblicz różnicę tego ciągu.
. Oblicz różnicę tego ciągu.
Ze zbioru liczb naturalnych czterocyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 11.
Liczby niezerowe 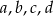 spełniają warunek
spełniają warunek 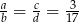 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 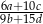 .
.
Stosunek długości przekątnych rombu o boku 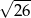 jest równy 3:2. Oblicz pole tego rombu.
jest równy 3:2. Oblicz pole tego rombu.
Dane są dwa przeciwległe wierzchołki 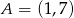 i
i 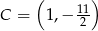 prostokąta
prostokąta 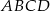 . Prosta o równaniu
. Prosta o równaniu 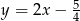 jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków
jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków 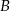 i
i 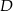 tego prostokąta.
tego prostokąta.
Podstawą ostrosłupa trójkątnego 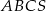 jest trójkąt prostokątny
jest trójkąt prostokątny 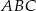 , w którym
, w którym 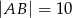 . Stosunek długości przyprostokątnej
. Stosunek długości przyprostokątnej 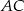 tego trójkąta do długości przyprostokątnej
tego trójkąta do długości przyprostokątnej 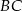 jest równy 4:3. Wszystkie krawędzie boczne ostrosłupa mają długość 13. Oblicz objętość tego ostrosłupa.
jest równy 4:3. Wszystkie krawędzie boczne ostrosłupa mają długość 13. Oblicz objętość tego ostrosłupa.