/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 10 kwietnia 2021 Czas pracy: 180 minut
Zadania zamknięte
Liczba 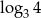 jest równa
jest równa
A) 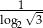 B)
B) 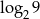 C)
C) 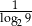 D)
D) 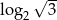
Granica 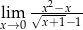 równa jest
równa jest
A) 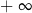 B)
B) 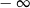 C) 0 D)
C) 0 D) 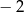
Mamy cztery urny. W urnie o numerze 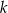 , dla
, dla 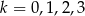 znajduje się
znajduje się 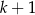 kul białych i
kul białych i 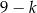 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z
kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z 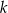 oczkami,
oczkami, 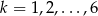 to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby
to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby 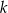 przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 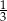 B)
B) 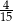 C)
C) 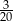 D)
D) 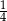
Liczba 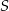 jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 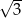 i ilorazie
i ilorazie 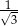 . Liczba
. Liczba 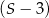 jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 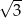 i ilorazie
i ilorazie 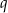 . Wynika stąd, że liczba
. Wynika stąd, że liczba 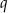 jest równa
jest równa
A) 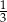 B)
B) 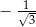 C)
C) 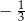 D)
D) 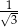
Zadania otwarte
Wykaż, że jeżeli prawdopodobieństwa zdarzeń 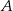 i
i 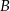 spełniają warunki:
spełniają warunki: 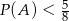 i
i 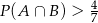 , to
, to
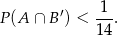
W czworokącie wypukłym 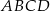 kąty przy wierzchołkach
kąty przy wierzchołkach 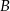 i
i 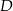 są proste (zobacz rysunek).
są proste (zobacz rysunek).
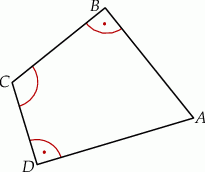
Oblicz sinus kąta przy wierzchołku 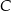 jeżeli
jeżeli 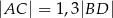 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 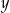 większej od 1 prawdziwa jest nierówność
większej od 1 prawdziwa jest nierówność 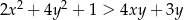 .
.
Rozwiąż równanie: 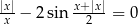 .
.
Dla jakich wartości parametru 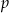 wielomian
wielomian 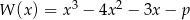 ma trzy pierwiastki rzeczywiste?
ma trzy pierwiastki rzeczywiste?
Na bokach 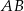 i
i 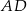 rombu
rombu 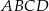 wybrano odpowiednio punkty
wybrano odpowiednio punkty 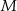 i
i 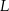 w ten sposób, że
w ten sposób, że 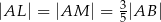 . Odcinek
. Odcinek 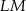 jest styczny do okręgu wpisanego w romb
jest styczny do okręgu wpisanego w romb 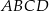 . Punkt
. Punkt 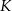 jest punktem styczności okręgu wpisanego w ten romb z bokiem
jest punktem styczności okręgu wpisanego w ten romb z bokiem 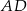 (zobacz rysunek).
(zobacz rysunek).
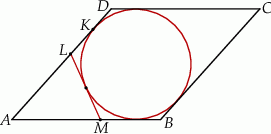
Wykaż, że 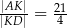 .
.
Wyznacz te wartości parametru 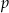 , dla których równanie
, dla których równanie 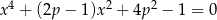 ma dokładnie dwa różne pierwiastki rzeczywiste.
ma dokładnie dwa różne pierwiastki rzeczywiste.
Czterowyrazowy ciąg 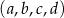 jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg
jest rosnący i arytmetyczny. Suma kwadratów trzech najmniejszych wyrazów tego ciągu jest pięciokrotnie większa od kwadratu czwartego wyrazu. Ponadto ciąg 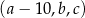 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 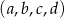 .
.
Każda krawędź graniastosłupa trójkątnego ma długość 26. Ściana boczna 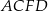 jest prostopadła do płaszczyzny podstawy
jest prostopadła do płaszczyzny podstawy 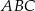 , a krawędź
, a krawędź 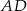 jest nachylona do płaszczyzny podstawy pod katem
jest nachylona do płaszczyzny podstawy pod katem  takim, że
takim, że 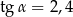 (zobacz rysunek).
(zobacz rysunek).
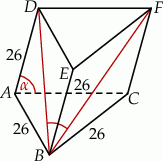
Oblicz cosinus kąta 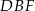 .
.
Odległość każdego z wierzchołków 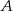 i
i 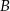 trójkąta
trójkąta 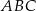 od punktu
od punktu 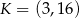 jest równa
jest równa 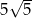 , a odległość tych wierzchołków od punktu
, a odległość tych wierzchołków od punktu 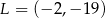 jest równa 25. Okrąg opisany na trójkącie
jest równa 25. Okrąg opisany na trójkącie 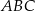 jest styczny do prostej
jest styczny do prostej 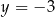 w punkcie
w punkcie 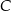 . Punkt
. Punkt 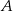 znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta
znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta 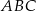 .
.
Należy zaprojektować wymiary prostokątnego placu zabaw, tak aby szerokość trawnika wzdłuż dłuższych brzegów placu była równa 1,5 m, a szerokość trawnika wzdłuż krótszych brzegów placu była równa 2,5 m (zobacz rysunek – plac zabaw zaznaczono kolorem szarym). Sam plac zabaw ma mieć powierzchnię 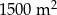 . Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.
. Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.