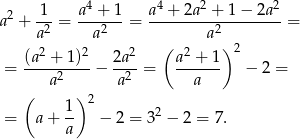Zadanie nr 5393255
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 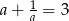 , to
, to 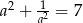 .
.
Rozwiązanie
Sposób I
Podnieśmy daną równość stronami do kwadratu
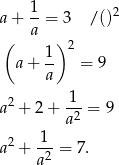
Sposób II
Przekształcamy lewą stronę
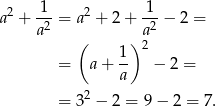
Sposób III
Przekształcamy lewą stronę
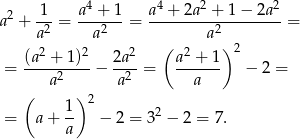
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 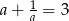 , to
, to 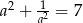 .
.
Sposób I
Podnieśmy daną równość stronami do kwadratu
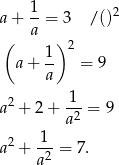
Sposób II
Przekształcamy lewą stronę
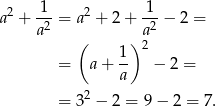
Sposób III
Przekształcamy lewą stronę