/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 9 maja 2020 Czas pracy: 170 minut
Zadania zamknięte
Funkcja wykładnicza określona wzorem  przyjmuje wartość 2 dla argumentu
przyjmuje wartość 2 dla argumentu
A) 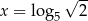 B)
B) 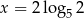 C)
C) 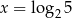 D)
D) 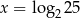
Liczba 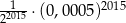 jest równa
jest równa
A) 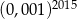 B)
B) 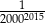 C)
C) 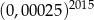 D)
D) 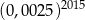
Wojtek 40% swoich oszczędności przeznaczył na zakup nowego plecaka. Połowę z tego, co mu zostało, przeznaczył na zakup butów. Ile procent oszczędności pozostało Wojtkowi?
A) 10% B) 30% C) 40% D) 20%
Ekipa złożona z 16 pracowników wykonała dach hali przemysłowej w ciągu 65 dni. Jeżeli dach na drugiej takiej samej hali trzeba wykonać w ciągu 52 dni, to, przy założeniu takiej samej wydajności, należy zatrudnić do pracy o
A) 2 osoby więcej. B) 4 osoby więcej. C) 6 osób więcej. D) 8 osób więcej.
Wskaż układ, który ma nieskończenie wiele rozwiązań.
A) 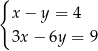 B)
B) 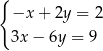 C)
C) 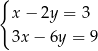 D)
D) 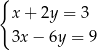
Równanie 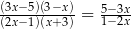 ma dwa rozwiązania. Są to liczby:
ma dwa rozwiązania. Są to liczby:
A) 3 i 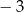 B) 3 i
B) 3 i  C) 0 i 3 D) 0 i
C) 0 i 3 D) 0 i 
Prostą o równaniu 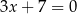 przekształcono w symetrii względem osi
przekształcono w symetrii względem osi 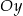 . W wyniku tego przekształcenia otrzymano prostą o równaniu
. W wyniku tego przekształcenia otrzymano prostą o równaniu
A) 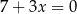 B)
B) 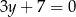 C)
C) 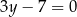 D)
D) 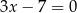
Osią symetrii paraboli będącej wykresem funkcji 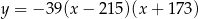 jest prosta o równaniu
jest prosta o równaniu
A) 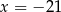 B)
B) 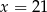 C)
C) 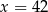 D)
D) 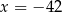
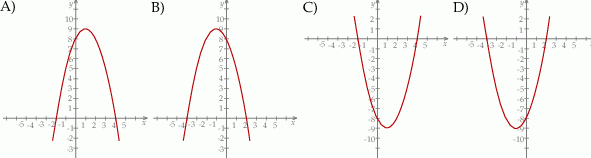
Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem 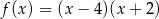 .
.
Liczbą odwrotną do 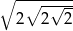 jest
jest
A) 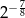 B)
B) 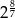 C)
C) 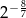 D)
D) 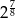
Pani Jolanta spłaciła kredyt w wysokości 20 000 zł w pięciu ratach, z których każda kolejna była o 600 zł mniejsza od poprzedniej. Pierwsza rata była równa:
A) 5 800 zł B) 4 800 zł C) 5 600 zł D) 5 200 zł
Jaką liczbę można wstawić pomiędzy liczby 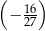 i
i 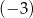 , aby z danymi liczbami tworzyła ciąg geometryczny?
, aby z danymi liczbami tworzyła ciąg geometryczny?
A) 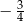 B)
B)  C)
C) 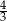 D)
D) 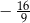
Liczba 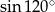 jest równa liczbie
jest równa liczbie
A) 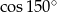 B)
B) 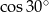 C)
C) 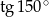 D)
D) 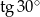
Punkt 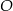 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
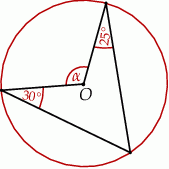
A) 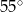 B)
B) 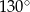 C)
C) 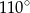 D)
D) 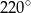
Dane są dwa okręgi o promieniach 10 i 18. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 18 B) 8 C) 10 D) 28
Pole trójkąta 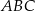 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
A) 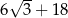 B)
B) 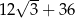 C)
C) 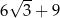 D)
D) 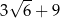
Dane jest równanie 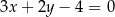 . Z którym z poniższych równań tworzy ono układ sprzeczny?
. Z którym z poniższych równań tworzy ono układ sprzeczny?
A) 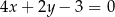 B)
B) 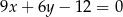 C)
C) 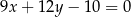 D)
D) 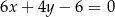
Dane są równania czterech prostych:
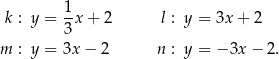
Prostopadłe są proste
A) 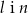 B)
B) 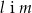 C)
C) 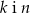 D)
D) 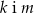
Funkcja 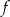 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb: 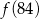 ,
, 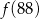 ,
, 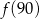 ,
, 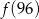 najmniejsza to
najmniejsza to
A) 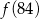 B)
B) 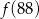 C)
C) 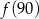 D)
D) 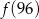
Równanie 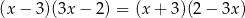 ma dwa rozwiązania. Są to liczby
ma dwa rozwiązania. Są to liczby
A) 0 oraz  B)
B) 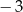 oraz
oraz  C)
C) 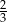 oraz 3 D)
oraz 3 D) 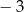 oraz 3
oraz 3
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
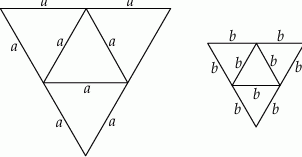
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 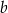 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 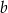 ?
?
A) 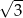 B)
B) 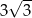 C) 3 D) 9
C) 3 D) 9
Z koła o promieniu 12 wycięto dwa wycinki odpowiadające kątom środkowym 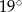 i
i 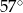 .
.
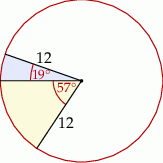
Następnie sklejono dwa stożki, których powierzchnie boczne utworzone zostały z otrzymanych wycinków. Ile razy pole podstawy większego z otrzymanych stożków jest większe od pola podstawy mniejszego stożka?
A) 3 B) 6 C) 9 D) 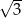
Samochód osobowy na dystansie 324 km spalił 20 litrów benzyny. Zakładając, że średnie zużycie paliwa nie ulegnie zmianie, ile benzyny spali ten samochód na dystansie 486 km?
A) 30 litrów. B) 28 litrów. C) 27 litrów. D) 32 litry.
Siedmiocyfrowe numery telefonów w pewnym mieście są tworzone z cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, przy czym numery nie mogą zaczynać się od cyfr 0, 1, 9. Ile najwięcej takich numerów telefonicznych można utworzyć?
A) 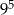 B)
B) 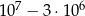 C)
C) 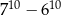 D)
D) 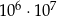
Rzucamy 10 razy symetryczną monetą. Niech 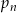 dla
dla 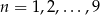 oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach
oznacza prawdopodobieństwo otrzymania dwóch orłów w rzutach o numerach  i
i 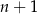 . Wtedy
. Wtedy
A) 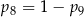 B)
B) 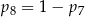 C)
C) 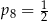 D)
D) 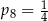
Zadania otwarte
Rozwiązaniem nierówności 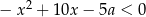 jest zbiór
jest zbiór 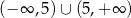 . Wyznacz
. Wyznacz  .
.
Rozwiąż równanie 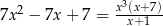 , dla
, dla 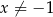 .
.
Udowodnij, że jeżeli 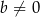 i
i 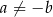 , to
, to 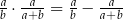 .
.
Na okręgu o promieniu  wybrano punkty
wybrano punkty 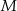 i
i 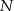 w ten sposób, że proste
w ten sposób, że proste 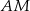 i
i 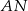 są styczne do okręgu. Punkt
są styczne do okręgu. Punkt 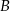 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 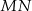 i prostej łączącej
i prostej łączącej 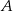 ze środkiem
ze środkiem 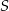 tego okręgu. Wykaż, że
tego okręgu. Wykaż, że 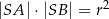 .
.
Ewa na początku 2015 roku kupiła skarbonkę i włożyła do niej 1000 zł. Na początku każdego kolejnego roku Ewa dokłada do skarbonki kwotę równą 20% dotychczas zgromadzonych oszczędności, a przez resztę roku nie dokłada, ani nie wybiera ze skarbonki żadnych pieniędzy. Ile będą wynosić oszczędności Ewy pod koniec roku 2020?
Wybieramy losowo 2 kostki z tabliczki czekolady przedstawionej na poniższym rysunku.

Oblicz prawdopodobieństwo tego, że wybrane dwie kostki są sąsiednie (tzn. mają wspólną krawędź).
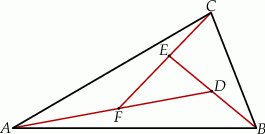
W trójkącie 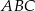 poprowadzono odcinki
poprowadzono odcinki 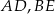 i
i 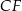 w ten sposób, że punkty
w ten sposób, że punkty 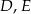 i
i 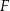 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 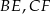 i
i 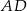 . Oblicz pole trójkąta
. Oblicz pole trójkąta 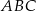 jeżeli pole trójkąta
jeżeli pole trójkąta 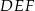 jest równe 2.
jest równe 2.
W prostokącie 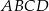 dane są
dane są 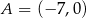 ,
, 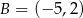 i
i 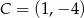 . Napisz równanie prostej, która jest styczna w punkcie
. Napisz równanie prostej, która jest styczna w punkcie 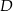 do okręgu opisanego na prostokącie
do okręgu opisanego na prostokącie 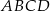 .
.
Dany jest ostrosłup prawidłowy czworokątny 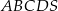 o podstawie
o podstawie 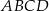 . Krawędź boczna tego ostrosłupa jest o
. Krawędź boczna tego ostrosłupa jest o 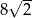 dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

