Zadanie nr 5560668
Punkty 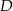 i
i 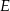 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 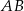 i ramienia
i ramienia 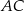 trójkąta równoramiennego
trójkąta równoramiennego 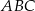 . Punkty
. Punkty 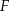 i
i 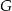 leżą na ramieniu
leżą na ramieniu 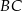 tak, że odcinki
tak, że odcinki 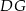 i
i 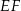 są prostopadłe do prostej
są prostopadłe do prostej 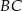 (zobacz rysunek).
(zobacz rysunek).
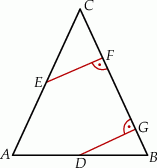
Pole trójkąta 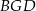 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 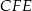 jest równe 4. Zatem pole trójkąta
jest równe 4. Zatem pole trójkąta 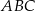 jest równe
jest równe
A) 24 B) 8 C) 12 D) 16
Rozwiązanie
Sposób I
Dorysujmy wysokość 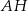 trójkąta
trójkąta  .
.
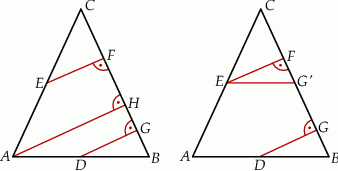
Zauważmy teraz, że trójkąt  jest podobny do trójkąta
jest podobny do trójkąta  w skali
w skali 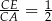 . Podobnie trójkąt
. Podobnie trójkąt 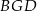 jest podobny do trójkąta
jest podobny do trójkąta 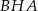 w skali
w skali 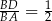 . Mamy stąd
. Mamy stąd
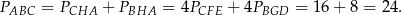
Sposób II
Niech 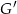 będzie takim punktem odcinka
będzie takim punktem odcinka 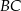 , że
, że 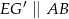 . Wtedy trójkąty
. Wtedy trójkąty 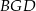 i
i 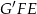 są podobne oraz
są podobne oraz 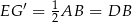 . Trójkąty te są więc przystające. Stąd
. Trójkąty te są więc przystające. Stąd
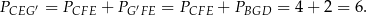
Teraz wystarczy zauważyć, że trójkąt 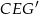 jest 2 razy mniejszy od trójkąta
jest 2 razy mniejszy od trójkąta 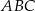 , więc
, więc
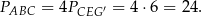
Odpowiedź: A

