/Szkoła średnia
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa I 14 maja 2019 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 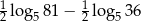 jest równa
jest równa
A) 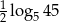 B)
B) 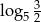 C)
C) 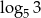 D)
D) 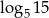
Liczba 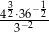 jest równa
jest równa
A) 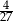 B) 8 C) 9 D) 12
B) 8 C) 9 D) 12
Wyrażenie 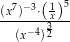 jest równe
jest równe
A) 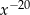 B)
B) 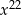 C)
C) 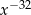 D)
D) 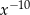
Wartość wyrażenia 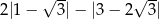 wynosi
wynosi
A) 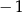 B)
B) 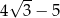 C) 1 D)
C) 1 D) 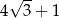
Liczbą przeciwną do liczby 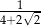 jest liczba
jest liczba
A) 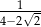 B)
B) 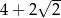 C)
C) 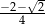 D)
D) 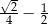
Cenę pewnego towaru podniesiono o 10%, a następnie obniżono o 15%. Cena po obu zmianach stanowi 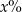 początkowej ceny towaru. Zatem
początkowej ceny towaru. Zatem
A) 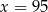 B)
B) 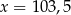 C)
C) 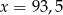 D)
D) 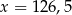
Do zbioru liczb wymiernych nie należy liczba
A) 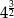 B)
B) 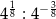 C)
C) 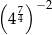 D)
D) 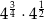
Jeżeli 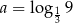 oraz
oraz 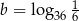 , to
, to
A) 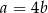 B)
B) 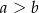 C)
C) 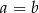 D)
D) 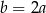
Ułamek 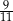 przybliżono z dokładnością do 0,01. Błąd względny tego przybliżenia wynosi
przybliżono z dokładnością do 0,01. Błąd względny tego przybliżenia wynosi
A) 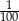 B)
B) 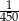 C)
C) 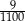 D)
D) 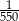
Wyrażenie 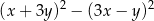 jest równe
jest równe
A) 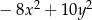 B)
B) 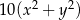 C)
C) 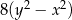 D)
D) 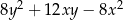
Dane są zbiory 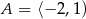 oraz
oraz 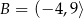 . Różnica
. Różnica 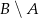 jest równa
jest równa
A) 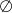 B)
B) 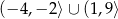 C)
C) 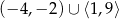 D)
D) 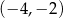
Rozwiązaniami równania 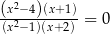 są liczby
są liczby
A) 2 B) 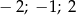 C)
C) 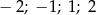 D)
D) 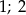
Układ równań 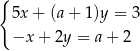 jest sprzeczny dla
jest sprzeczny dla  równego
równego
A) 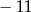 B) 9 C) 4 D)
B) 9 C) 4 D) 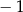
Do zbioru rozwiązań nierówności 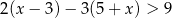 należy liczba
należy liczba
A) 30 B) 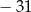 C)
C) 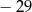 D)
D) 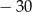
Dziedziną funkcji 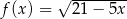 jest zbiór
jest zbiór
A) 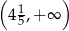 B)
B) 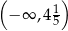 C)
C) 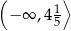 D)
D) 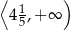
Funkcja 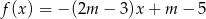 przyjmuje wartość
przyjmuje wartość 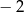 dla argumentu równego
dla argumentu równego 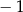 .
.
A) 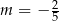 B)
B) 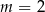 C)
C) 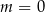 D)
D) 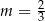
Wartość wyrażenia 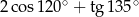 jest równa
jest równa
A) 2 B) 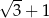 C)
C) 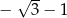 D)
D) 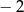
Jedna z przyprostokątnych w trójkącie prostokątnym ma długość 3 cm, a przeciwprostokątna 4 cm. Najmniejszym kątem tego trójkąta jest  . Wartość wyrażenia
. Wartość wyrażenia 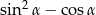 wynosi
wynosi
A) 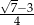 B)
B) 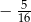 C)
C) 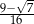 D) 1
D) 1
Jeden z kątów ostrych trójkąta prostokątnego ma miarę 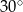 . Dłuższa przyprostokątna tego trójkąta ma długość 6 cm. Promień okręgu opisanego na tym trójkącie ma długość
. Dłuższa przyprostokątna tego trójkąta ma długość 6 cm. Promień okręgu opisanego na tym trójkącie ma długość
A) 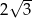 B) 6 C)
B) 6 C) 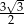 D)
D) 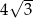
Punkt 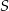 jest środkiem okręgu.
jest środkiem okręgu.
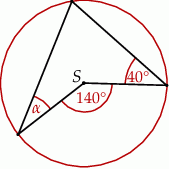
Miara kąta  wynosi
wynosi
A) 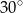 B)
B) 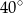 C)
C) 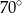 D)
D) 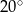
Obwód trójkąta prostokątnego równoramiennego wynosi 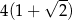 . Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
. Długość wysokości poprowadzonej z wierzchołka kąta prostego tego trójkąta jest równa
A) 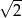 B) 4 C) 2 D)
B) 4 C) 2 D) 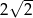
Punkty 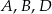 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 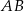 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego 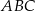 (zobacz rysunek).
(zobacz rysunek).
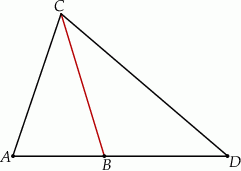
Jeżeli 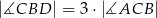 , to
, to 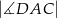 wynosi
wynosi
A) 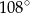 B)
B) 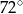 C)
C) 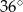 D)
D) 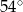
Najkrótszy bok trójkąta prostokątnego ma długość 5 cm, a najdłuższy 13 cm. Pole tego trójkąta jest równe
A) 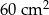 B)
B) 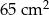 C)
C) 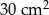 D)
D) 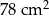
Ramię trójkąta równoramiennego 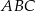 ma długość 8, a jeden z kątów tego trójkąta ma miarę
ma długość 8, a jeden z kątów tego trójkąta ma miarę 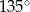 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 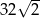 B)
B) 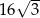 C) 32 D)
C) 32 D) 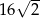
Trójkąt 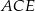 jest prostokątny oraz
jest prostokątny oraz 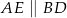 (zobacz rysunek).
(zobacz rysunek).
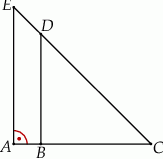
Jeżeli 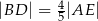 oraz
oraz 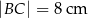 , to
, to
A) 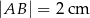 B)
B) 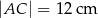 C)
C) 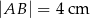 D)
D) 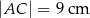
Zadania otwarte
Rozwiąż równanie 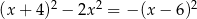 .
.
Wykaż, że liczba 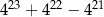 jest podzielna przez 38.
jest podzielna przez 38.
Początkowe ramię kąta  pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt
pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt 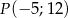 . Oblicz wartość wyrażenia:
. Oblicz wartość wyrażenia: 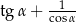 .
.
Wykaż, że w dowolnym trapezie suma długości podstaw jest mniejsza od sumy długości przekątnych.
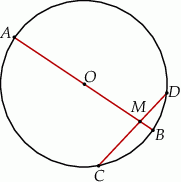
Cięciwa 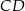 okręgu o środku
okręgu o środku 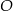 przecina średnicę
przecina średnicę 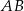 tego okręgu w punkcie
tego okręgu w punkcie 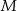 (rysunek). Kąt środkowy oparty na łuku
(rysunek). Kąt środkowy oparty na łuku 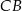 ma miarę
ma miarę 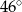 , a
, a 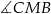 ma miarę
ma miarę 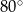 . Oblicz
. Oblicz 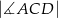 .
.
Wyznacz iloczyn (część wspólną) zbiorów rozwiązań nierówności: 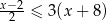 oraz
oraz 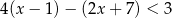 .
.
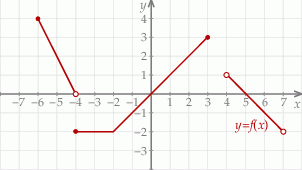
Poniżej przedstawiony jest wykres funkcji 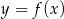 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
- wartość wyrażenia
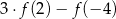 ,
, - dziedzinę funkcji
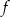 ,
, - maksymalne przedziały, w których funkcja
 jest malejąca,
jest malejąca, - zbiór argumentów, dla których funkcja
 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne.
Dane są dwie liczby dodatnie  i
i 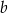 , których stosunek wynosi 4:5. Jeżeli mniejszą z tych liczb zwiększymy o 25%, a większą zmniejszymy o 40, to stosunek otrzymanych liczb wyniesie 3:2. Oblicz wartość wyrażenia:
, których stosunek wynosi 4:5. Jeżeli mniejszą z tych liczb zwiększymy o 25%, a większą zmniejszymy o 40, to stosunek otrzymanych liczb wyniesie 3:2. Oblicz wartość wyrażenia: 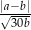 .
.
Bok 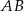 trójkąta
trójkąta 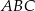 jest średnicą okręgu opisanego na tym trójkącie. Bok
jest średnicą okręgu opisanego na tym trójkącie. Bok 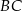 jest o 4 cm krótszy od boku
jest o 4 cm krótszy od boku 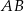 oraz
oraz 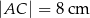 . Oblicz pole trójkąta
. Oblicz pole trójkąta 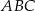 oraz długość promienia okręgu wpisanego w ten trójkąt.
oraz długość promienia okręgu wpisanego w ten trójkąt.

