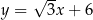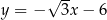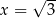Zadanie nr 5615298
W kartezjańskim układzie współrzędnych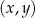 
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta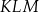 
. Trójkąt 
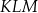jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 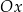 jest osią symetrii tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | jedna z tych prostych jest równoległa do osi  . |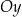
Rozwiązanie
Zauważmy, że równania pierwszej i drugiej prostej różnią się znakiem, co oznacza, że te dwie proste są symetryczne względem osi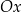 
. Ponadto trzecia prosta jest pionowa. Gdy to naszkicujemy to widać, że trójkąt 
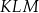jest równoramienny.
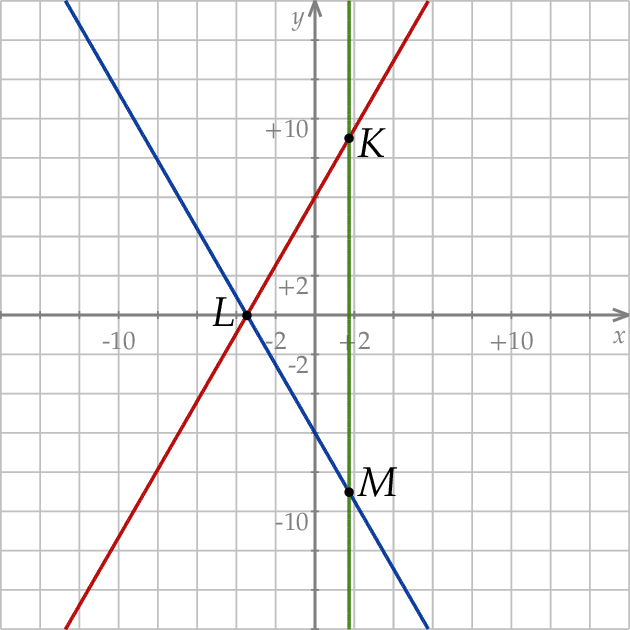
Odpowiedź: A, 1
