Zadanie nr 5640225
Z urny, w której jest 7 kul czarnych i 3 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule różnych kolorów.
Rozwiązanie
Najpierw obliczmy na ile sposobów możemy wyciągnąć 2 kule
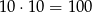
(kule zwracamy więc za każdym razem losujemy spośród 10 kul).
Sposób I
Zastanówmy się jakie będą zdarzenia sprzyjające. Dwie różne kule możemy wylosować na
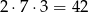
sposoby (mnożymy przez dwa bo możemy wylosować kulę czarną a następnie żółtą, albo najpierw żółtą, a później czarną). Zatem interesujące nas prawdopodobieństwo wynosi
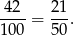
Sposób II
Obliczymy prawdopodobieństwo zdarzenia przeciwnego tzn. prawdopodobieństwo wylosowania dwóch kul w tym samym kolorze.
Po pierwsze, możemy wyciągnąć 2 kule czarne. Możemy zrobić to na
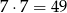
sposobów. Druga możliwa sytuacja to wylosowanie 2 kul żółtych. Możemy zrobić to na
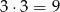
sposobów. Zatem prawdopodobieństwo wylosowania dwóch kul w różnych kolorach wynosi
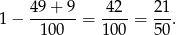
Odpowiedź: