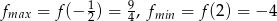/Szkoła średnia

Zadanie nr 5663719

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz najmniejszą i największą wartość funkcji 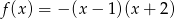f(x) = −(x − 1 )(x+ 2) w przedziale ⟨− 1;2 ⟩ .

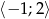Rozwiązanie

Ramiona paraboli są skierowane w dół, więc wartość największa jest przyjmowana w jej wierzchołku (jeżeli jest w podanym przedziale), a wartość najmniejsza w jednym z końców przedziału. W którym? – policzymy i sprawdzimy.

Wierzchołek paraboli znajduje się dokładnie pomiędzy pierwiastkami, czyli w punkcie

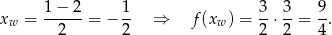
1 − 2 1 3 3 9 xw = ------= − -- ⇒ f (xw) = --⋅--= -. 2 2 2 2 4

Sprawdźmy jeszcze końce przedziału.

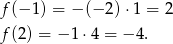
f (−1 ) = − (− 2)⋅1 = 2 f (2) = − 1⋅4 = − 4.

Na koniec obrazek.

PIC

 
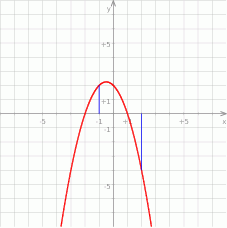
Odpowiedź: fmax = f(− 12) = 94 , fmin = f (2) = − 4

Wersja PDF