/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 29 lutego 2020 Czas pracy: 170 minut
Zadania zamknięte
Jedną trzecią dodatniej liczby  zwiększono o 20%. Otrzymano w ten sposób
zwiększono o 20%. Otrzymano w ten sposób
A) 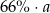 B)
B) 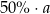 C)
C) 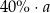 D)
D) 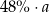
Liczba 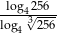 jest równa
jest równa
A) 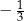 B)
B) 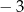 C) 3 D)
C) 3 D) 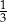
Liczba 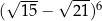 jest równa liczbie
jest równa liczbie
A) 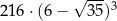 B)
B) 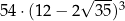 C)
C) 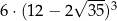 D)
D) 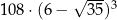
Równość 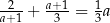 jest prawdziwa dla liczby wymiernej
jest prawdziwa dla liczby wymiernej
A) 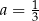 B)
B) 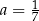 C)
C) 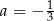 D)
D) 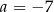
Funkcja liniowa 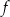 jest określona wzorem
jest określona wzorem 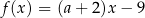 , gdzie
, gdzie  to pewna liczba rzeczywista. Wykres funkcji
to pewna liczba rzeczywista. Wykres funkcji 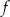 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 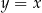 . Stąd wynika, że
. Stąd wynika, że
A) 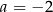 B)
B) 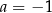 C)
C) 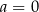 D)
D) 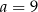
Równanie 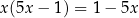 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 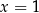 . B) dwa rozwiązania:
. B) dwa rozwiązania: 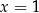 i
i 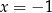 .
.
C) dwa rozwiązania: 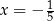 i
i 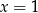 . D) dwa rozwiązania:
. D) dwa rozwiązania: 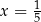 i
i 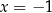 .
.
Liczbę 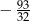 zaokrąglamy do najbliższej liczby całkowitej. Błąd bezwzględny tego przybliżenia jest równy
zaokrąglamy do najbliższej liczby całkowitej. Błąd bezwzględny tego przybliżenia jest równy
A) 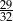 B)
B) 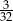 C)
C) 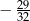 D)
D) 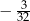
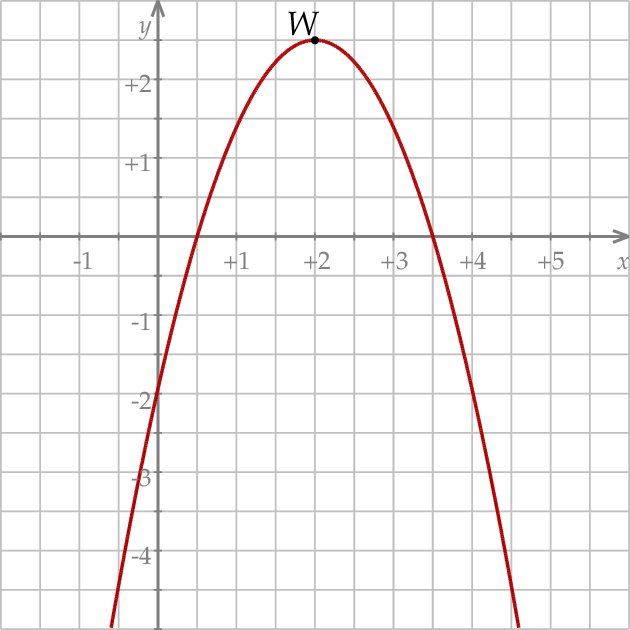
Informacja do zadań 8 – 10
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 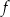 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 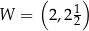 . Liczby
. Liczby 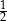 i
i 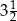 to miejsca zerowe funkcji
to miejsca zerowe funkcji 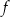 .
.
Zbiorem wartości funkcji 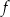 jest przedział
jest przedział
A) 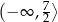 B)
B) 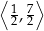 C)
C) 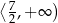 D)
D) 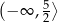
Najmniejsza wartość funkcji 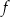 w przedziale
w przedziale 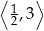 jest równa
jest równa
A) 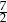 B)
B)  C) 0 D)
C) 0 D) 
Osią symetrii wykresu funkcji 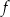 jest prosta o równaniu
jest prosta o równaniu
A) 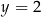 B)
B) 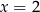 C)
C) 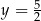 D)
D) 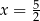
Dany jest rosnący ciąg geometryczny 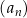 , określony dla liczb naturalnych
, określony dla liczb naturalnych 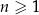 , o wyrazach dodatnich. Jeśli
, o wyrazach dodatnich. Jeśli 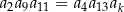 , to
, to 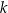 jest równe
jest równe
A) 8 B) 7 C) 6 D) 5
W ciągu arytmetycznym 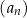 , określonym dla
, określonym dla 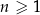 , dane są dwa wyrazy:
, dane są dwa wyrazy: 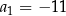 oraz
oraz 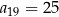 . Wtedy suma
. Wtedy suma
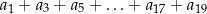
jest równa
A) 133 B) 63 C) 70 D) 49
Kąt  jest rozwarty i
jest rozwarty i 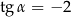 . Wobec tego
. Wobec tego
A) 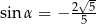 B)
B) 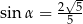 C)
C) 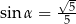 D)
D) 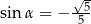
Punkty 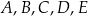 leżą na okręgu o środku
leżą na okręgu o środku 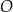 , przy czym
, przy czym 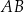 jest średnicą tego okręgu,
jest średnicą tego okręgu, 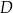 jest środkiem łuku
jest środkiem łuku 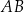 oraz
oraz 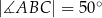 .
.
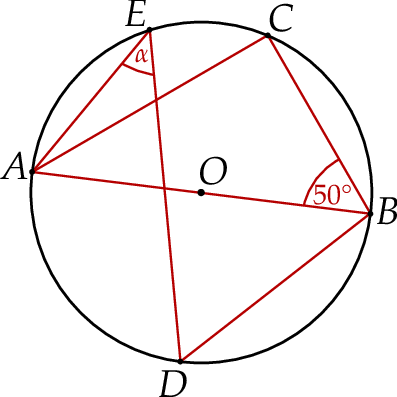
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 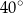 B)
B) 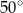 C)
C) 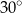 D)
D) 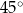
Pole trójkąta 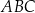 o wierzchołkach
o wierzchołkach 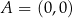 ,
, 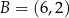 ,
, 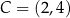 jest równe
jest równe
A) 10 B) 5 C) 20 D) 15
Równanie 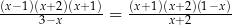
A) ma cztery różne rozwiązania: 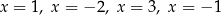 .
.
B) ma trzy różne rozwiązania: 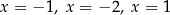 .
.
C) ma dwa różne rozwiązania: 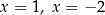 .
.
D) ma dwa różne rozwiązania: 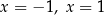 .
.
Jeżeli 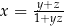 i
i 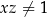 , to
, to
A) 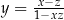 B)
B) 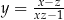 C)
C) 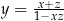 D)
D) 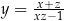
Prosta o równaniu 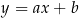 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 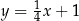 i przechodzi przez punkt
i przechodzi przez punkt 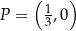 , gdy
, gdy
A) 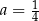 i
i 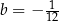 B)
B) 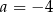 i
i 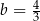
C) 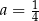 i
i 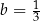 D)
D) 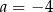 i
i 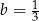
W układzie współrzędnych dany jest równoległobok 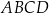 o wierzchołkach
o wierzchołkach 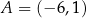 ,
, 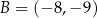 ,
, 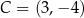 i
i 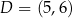 . Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
. Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
A) 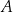 B)
B) 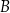 C)
C) 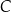 D)
D) 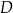
Dany jest trójkąt równoramienny 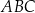 , w którym
, w którym 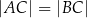 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 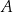 przecina bok
przecina bok 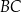 tego trójkąta w punkcie
tego trójkąta w punkcie 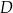 . Kąt
. Kąt 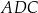 ma miarę
ma miarę 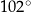 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę
A) 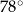 B)
B) 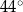 C)
C) 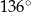 D)
D) 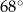
Ile jest wszystkich pięciocyfrowych liczb naturalnych podzielnych przez 29?
A) 3103 B) 3105 C) 3104 D) 3106
Promień kuli jest równy promieniowi podstawy walca, oraz objętości obu brył są równe. Stosunek pola powierzchni kuli do pola powierzchni całkowitej walca jest równy
A) 1 B)  C)
C)  D)
D) 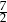
Dany jest sześcian 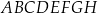 . Przekątne
. Przekątne 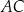 i
i 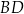 ściany
ściany 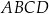 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 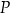 (zobacz rysunek).
(zobacz rysunek).
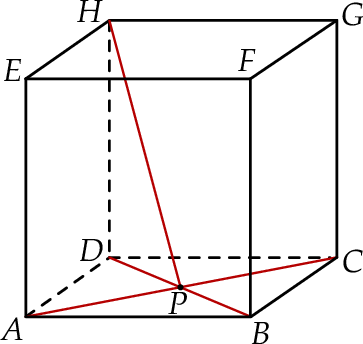
Tangens kąta, jaki odcinek 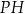 tworzy z krawędzią
tworzy z krawędzią 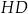 , jest równy
, jest równy
A) 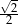 B)
B) 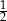 C) 1 D)
C) 1 D) 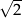
Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy długości 80 cm i krawędzi bocznej długości 90 cm (zobacz rysunek), a ponadto dane są cztery odcinki 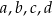 , o długościach – odpowiednio – 53 cm, 59 cm, 63 cm i 69 cm.
, o długościach – odpowiednio – 53 cm, 59 cm, 63 cm i 69 cm.
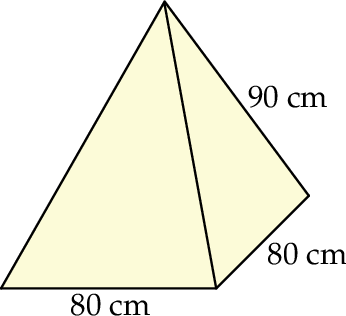
Wysokość tego ostrosłupa jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 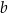 .
.
C) tylko od odcinków 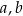 i
i  .
.
D) od wszystkich czterech danych odcinków.
W pudełku znajdują się dwie kule: niebieska i czerwona. Ośmiokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie siedem z wylosowanych kul jest tego samego koloru jest równe
A) 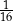 B)
B) 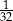 C)
C) 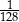 D)
D) 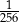
Zadania otwarte
Rozwiąż równanie 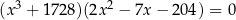 .
.
Rozwiąż nierówność 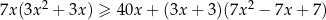 .
.
Funkcja kwadratowa  , spełnia warunek
, spełnia warunek 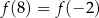 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  , spełniony jest warunek
, spełniony jest warunek 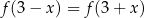 .
.
W trapezie 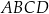 punkt
punkt 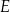 jest środkiem boku
jest środkiem boku 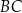 oraz
oraz 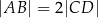 . Z wierzchołka
. Z wierzchołka 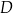 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 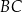 w punkcie
w punkcie 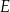 . Proste
. Proste 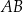 i
i 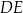 przecinają się w punkcie
przecinają się w punkcie 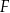 (zobacz rysunek).
(zobacz rysunek).
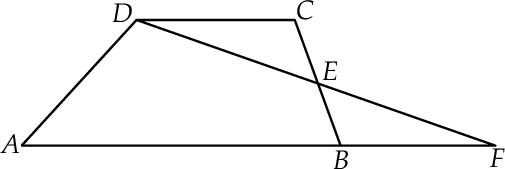
Wykaż, pole trójkąta 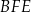 jest pięć razy mniejsze od pola czworokąta
jest pięć razy mniejsze od pola czworokąta 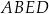 .
.
Ze zbioru liczb 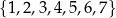 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 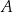 polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
Suma ośmiu początkowych wyrazów ciągu arytmetycznego 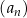 , określonego dla
, określonego dla 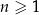 , jest równa 90, a suma
, jest równa 90, a suma 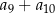 jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
Dwa boki kwadratu zawierają się w prostych o równaniach 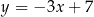 i
i 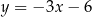 . Oblicz pole tego kwadratu.
. Oblicz pole tego kwadratu.
Liczby rzeczywiste 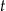 i
i 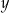 spełniają warunek
spełniają warunek 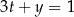 . Wyznacz takie wartości
. Wyznacz takie wartości 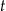 i
i 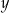 , dla których wyrażenie
, dla których wyrażenie 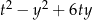 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Kąt  jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli
jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli 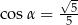 .
.