/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 14 marca 2015 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 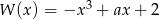 jest podzielny przez dwumian
jest podzielny przez dwumian 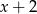 . Wynika stąd, że
. Wynika stąd, że
A) 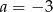 B)
B) 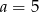 C)
C) 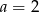 D)
D) 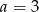
Granica
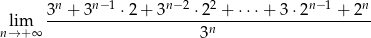
jest równa
A) 2 B) 3 C)  D) 0
D) 0
Największa wartość funkcji 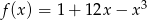
A) jest równa 17 B) jest równa 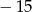 C) jest równa 4 D) nie istnieje
C) jest równa 4 D) nie istnieje
Kasia przygotowała 6 karteczek w ten sposób, że na każdej karteczce napisana jest jedna cyfra. Ile różnych liczb 6 cyfrowych można utworzyć kładąc obok siebie te karteczki, jeżeli na karteczkach napisane są cyfry: 1, 1, 2, 3, 4, 5?
A) 120 B) 320 C) 360 D) 720
Funkcje 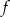 i
i 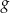 są określone dla wszystkich liczb rzeczywistych
są określone dla wszystkich liczb rzeczywistych 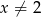 wzorami:
wzorami: 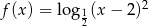 ,
, 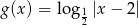 . Ile punktów wspólnych mają wykresy tych funkcji?
. Ile punktów wspólnych mają wykresy tych funkcji?
A) 0 B) 1 C) 2 D) 4
Zadania otwarte
Dany jest kwadrat 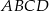 o boku długości 2. Punkt
o boku długości 2. Punkt 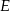 jest punktem przekątnej
jest punktem przekątnej 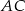 , takim że
, takim że 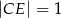 . Oblicz długość odcinka
. Oblicz długość odcinka 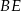 .
.
Oblicz granicę jednostronną 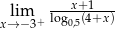 .
.
Dana jest funkcja 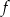 określona wzorem
określona wzorem 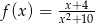 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej  . Oblicz wartość pochodnej tej funkcji w punkcie
. Oblicz wartość pochodnej tej funkcji w punkcie 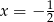 .
.
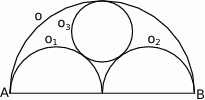
W półkolu  o średnicy
o średnicy 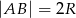 narysowano dwa przystające i zewnętrznie styczne półkola
narysowano dwa przystające i zewnętrznie styczne półkola 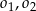 , których środki leżą na odcinku
, których środki leżą na odcinku 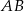 , i które są wewnętrznie styczne do półkola
, i które są wewnętrznie styczne do półkola  . Oblicz promień okręgu
. Oblicz promień okręgu 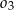 , który jest styczny do
, który jest styczny do 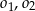 i
i  .
.
Oblicz, ile jest punktów 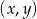 na płaszczyźnie, których współrzędne
na płaszczyźnie, których współrzędne  i
i 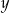 są liczbami całkowitymi spełniającymi odpowiednio nierówności:
są liczbami całkowitymi spełniającymi odpowiednio nierówności: 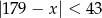 i
i 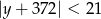 .
.
Dany jest prostopadłościan o polu powierzchni równym 162, w którym przekątna jest liczbą z przedziału 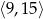 . Wykaż, że suma długości wszystkich krawędzi tego prostopadłościanu jest liczbą z przedziału
. Wykaż, że suma długości wszystkich krawędzi tego prostopadłościanu jest liczbą z przedziału 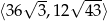 .
.
Wyznacz równanie stycznej do wykresu funkcji 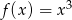 , która przecina oś
, która przecina oś 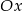 w jednym punkcie:
w jednym punkcie: 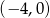 .
.
Liczby  i
i 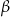 są pierwiastkami równania
są pierwiastkami równania 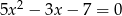 . Wykaż, że pierwiastkami równania
. Wykaż, że pierwiastkami równania 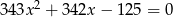 są liczby
są liczby 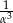 i
i 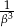 .
.
Wyznacz wszystkie wartości parametru 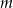 , dla których prosta o równaniu
, dla których prosta o równaniu 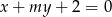 ma dokładnie dwa punkty wspólne z parabolą o równaniu
ma dokładnie dwa punkty wspólne z parabolą o równaniu 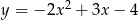 .
.
Rozwiąż równanie 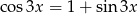 .
.
W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość  . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę
. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę 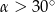 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Sześć ponumerowanych kul rozmieszczamy losowo w 5 pudełkach. Jakie jest prawdopodobieństwo, że dokładnie dwa pudełka będą puste?
Na wykresie funkcji 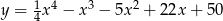 znajdź współrzędne punktu
znajdź współrzędne punktu 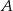 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 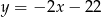 jest najmniejsza.
jest najmniejsza.

