/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 28 marca 2020 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 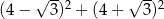 wynosi
wynosi
A) 19 B) 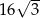 C) 32 D) 38
C) 32 D) 38
Liczba 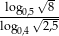 jest równa
jest równa
A) 3 B)  C)
C) 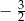 D)
D) 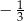
W wyniku dwóch obniżek cenę spodni obniżono o 52%. W ramach pierwszej z tych obniżek cenę zmniejszono o 20%. O ile procent zmniejszono cenę w ramach drugiej obniżki?
A) o 60% B) o 40% C) o 20% D) o 50%
Równość 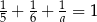 jest prawdziwa dla
jest prawdziwa dla
A) 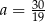 B)
B) 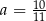 C)
C) 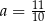 D)
D) 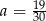
Funkcja kwadratowa 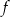 jest określona wzorem
jest określona wzorem 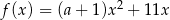 , gdzie
, gdzie  to pewna liczba rzeczywista. Liczba
to pewna liczba rzeczywista. Liczba 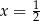 jest miejscem zerowym tej funkcji. Stąd wynika, że
jest miejscem zerowym tej funkcji. Stąd wynika, że
A) 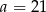 B)
B) 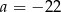 C)
C) 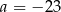 D)
D) 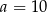
Liczba rzeczywistych rozwiązań równania 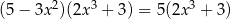 jest równa
jest równa
A) 5 B) 3 C) 2 D) 4
Dla pewnych liczb  i
i 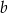 zachodzą równości:
zachodzą równości: 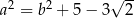 i
i 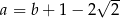 . Wartość wyrażenia
. Wartość wyrażenia  jest równa
jest równa
A) 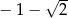 B)
B) 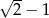 C)
C) 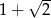 D)
D) 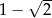
Informacja do zadań 8 i 9
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 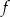 , określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty
, określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty 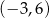 i
i 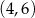 , a liczba
, a liczba 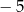 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 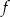 .
.
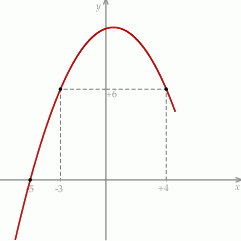
Drugim miejscem zerowym funkcji 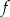 jest liczba
jest liczba
A) 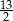 B) 6 C)
B) 6 C) 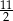 D) 5
D) 5
Największa wartość funkcji w przedziale 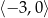 , to
, to
A) 10 B) 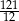 C)
C) 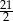 D) 9
D) 9
Dany jest rosnący ciąg arytmetyczny 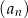 , określony dla liczb naturalnych
, określony dla liczb naturalnych 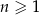 , o wyrazach dodatnich. Jeśli
, o wyrazach dodatnich. Jeśli 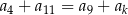 , to
, to  jest równe
jest równe
A) 8 B) 7 C) 6 D) 5
Dany jest ciąg geometryczny 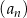 , określony dla
, określony dla 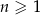 , w którym
, w którym 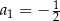 ,
, 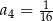 . Suma czterech początkowych wyrazów ciągu
. Suma czterech początkowych wyrazów ciągu 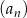 jest równa
jest równa
A) 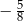 B)
B) 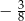 C)
C) 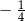 D)
D) 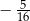
Na rysunku przedstawiono wykres funkcji 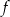 .
.
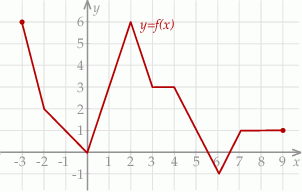
Najdłuższy przedział, na którym funkcja 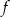 jest malejąca to
jest malejąca to
A) 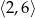 B)
B) 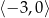 C)
C) 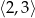 D)
D) 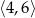
Cosinus kąta rozwartego  jest równy
jest równy 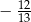 . Wtedy
. Wtedy
A) 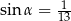 B)
B) 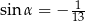 C)
C) 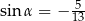 D)
D) 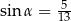
Na okręgu opisanym na kwadracie 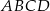 wybrano punkt
wybrano punkt 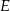 w ten sposób, że
w ten sposób, że 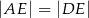 .
.
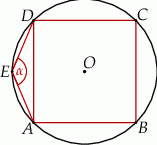
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 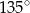 B)
B) 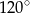 C)
C) 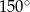 D)
D) 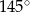
Punkty 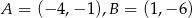 i
i 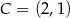 są trzema kolejnymi wierzchołkami rombu
są trzema kolejnymi wierzchołkami rombu 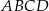 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 40 B) 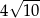 C) 80 D) 20
C) 80 D) 20
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pary liczb 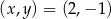 i
i 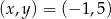 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 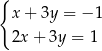 B)
B) 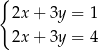 C)
C) 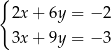 D)
D) 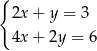
W urnie zawierającej kule białe i czarne jest 60 kul. Losujemy jedną kulę. Jeśli prawdopodobieństwo wylosowania kuli białej jest równe 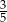 , to kul czarnych w tej urnie jest
, to kul czarnych w tej urnie jest
A) 30 B) 24 C) 20 D) 36
Prosta 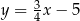 jest osią symetrii trójkąta
jest osią symetrii trójkąta 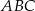 , w którym
, w którym 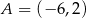 i
i 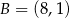 . Bok
. Bok 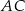 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu
A) 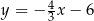 B)
B) 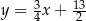 C)
C) 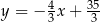 D)
D) 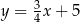
W układzie współrzędnych na płaszczyźnie danych jest 5 punktów: 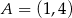 ,
, 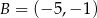 ,
, 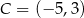 ,
, 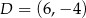 ,
, 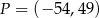 . Punkt
. Punkt 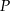 należy do tej samej ćwiartki układu współrzędnych co punkt
należy do tej samej ćwiartki układu współrzędnych co punkt
A) 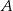 B)
B) 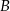 C)
C) 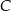 D)
D) 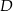
Odcinek 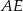 jest dwusieczną kąta
jest dwusieczną kąta 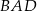 w równoległoboku
w równoległoboku 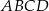 . Miara kąta
. Miara kąta 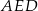 jest równa
jest równa 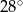 .
.
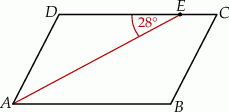
Miara kąta 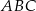 jest równa
jest równa
A) 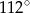 B)
B) 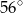 C)
C) 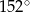 D)
D) 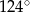
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 6 i niepodzielnych przez 4?
A) 150 B) 75 C) 83 D) 68
Pole powierzchni kuli o promieniu 6 cm jest równe polu powierzchni całkowitej stożka o promieniu podstawy 8 cm. Pole powierzchni bocznej stożka jest równe
A) 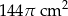 B)
B) 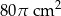 C)
C) 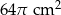 D)
D) 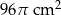
Dany jest sześcian 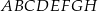 . Przekątne
. Przekątne 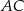 i
i 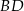 ściany
ściany 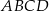 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 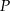 (zobacz rysunek).
(zobacz rysunek).
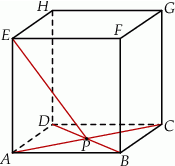
Tangens kąta, jaki odcinek 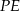 tworzy z płaszczyzną
tworzy z płaszczyzną 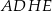 , jest równy
, jest równy
A) 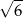 B)
B) 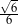 C)
C) 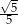 D)
D) 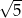
Dany jest prostopadłościan o wymiarach 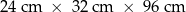 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 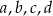 , o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
, o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
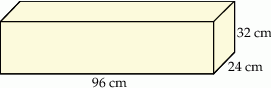
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 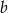 .
.
C) tylko od odcinków 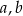 i
i  .
.
D) od wszystkich czterech danych odcinków.
Mediana dziesięciu liczb naturalnych: 3, 10, 5,  ,
,  ,
,  ,
,  , 12, 19, 7 jest równa 14. Średnia arytmetyczna tych liczb jest równa
, 12, 19, 7 jest równa 14. Średnia arytmetyczna tych liczb jest równa
A) 16 B) 12 C) 12,2 D) 14
Zadania otwarte
Rozwiąż równanie 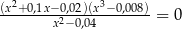 .
.
Rozwiąż nierówność 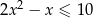 .
.
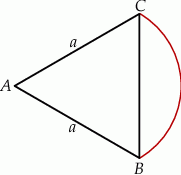
Trójkąt 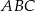 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami
. Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami 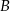 i
i 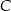 ma długość większą niż
ma długość większą niż 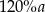 .
.
Wykaż, że jeżeli liczby rzeczywiste  i
i 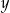 spełniają warunek
spełniają warunek
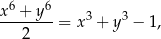
to 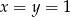 .
.
Ze zbioru wszystkich liczb trzycyfrowych losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 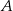 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Przekątne rombu 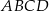 przecinają się w punkcie
przecinają się w punkcie 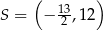 . Punkty
. Punkty 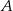 i
i 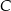 leżą na prostej o równaniu
leżą na prostej o równaniu 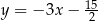 . Wyznacz równanie prostej
. Wyznacz równanie prostej 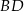 .
.
Środek okręgu leży w odległości 8 cm od cięciwy tego okręgu. Długość tej cięciwy jest o 13 cm większa od promienia tego okręgu. Oblicz promień tego okręgu.
Liczby rzeczywiste  i
i  spełniają warunek
spełniają warunek 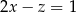 . Wyznacz takie wartości
. Wyznacz takie wartości  i
i  , dla których wyrażenie
, dla których wyrażenie 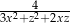 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
W ostrosłupie prawidłowym trójkątnym 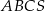 krawędź podstawy ma długość 12, a jego objętość jest równa
krawędź podstawy ma długość 12, a jego objętość jest równa 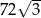 . Kąt
. Kąt  jest kątem między krawędziami bocznymi
jest kątem między krawędziami bocznymi 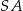 i
i 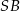 (zobacz rysunek). Oblicz sinus kąta
(zobacz rysunek). Oblicz sinus kąta  .
.