Zadanie nr 6580563
Dla jakich wartości parametru 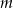 miejsca zerowe funkcji
miejsca zerowe funkcji 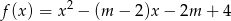 należą do przedziału
należą do przedziału 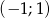 ?
?
Rozwiązanie
Na początek sprawdźmy, kiedy podana funkcja ma miejsca zerowe.
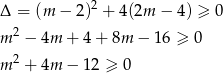
Rozwiązujemy tę nierówność kwadratową
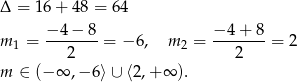
Dalszą część rozwiązania przeprowadzimy na dwa sposoby.
Sposób I
Ponieważ wykresem funkcji 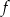 jest parabola o ramionach skierowanych w górę, to podany warunek jest równoważny temu, że wierzchołek paraboli jest zawarty w podanym przedziale oraz wartości funkcji na końcach przedziału są dodatnie (patrz rysunek).
jest parabola o ramionach skierowanych w górę, to podany warunek jest równoważny temu, że wierzchołek paraboli jest zawarty w podanym przedziale oraz wartości funkcji na końcach przedziału są dodatnie (patrz rysunek).
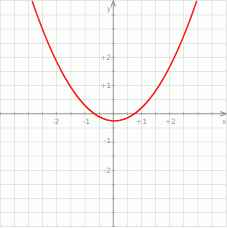
Mamy zatem układ nierówności
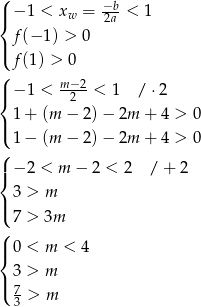
Mamy stąd 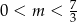 . W połączeniu z wcześniej wyliczonym warunkiem na
. W połączeniu z wcześniej wyliczonym warunkiem na 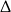 -ę, mamy więc
-ę, mamy więc
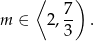
Sposób II
Sprawdziliśmy już, kiedy funkcja 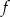 ma miejsca zerowe, sprawdźmy teraz kiedy są one w przedziale
ma miejsca zerowe, sprawdźmy teraz kiedy są one w przedziale 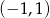 .
.
Zacznijmy od przypadku 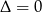 , czyli
, czyli 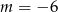 lub
lub 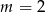 . Mamy wtedy odpowiednio funkcje
. Mamy wtedy odpowiednio funkcje
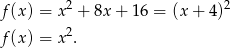
Tylko druga z tych funkcji spełnia warunki zadania.
Jeżeli natomiast 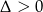 to równanie ma dwa pierwiastki
to równanie ma dwa pierwiastki 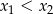 , które muszą spełniać warunki
, które muszą spełniać warunki
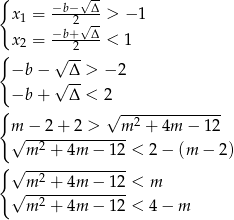
Jeżeli prawa strona którejkolwiek z powyższych nierówności jest ujemna, to otrzymujemy nierówność sprzeczną, więc musimy założyć, że 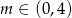 . Przy tym założeniu możemy podnieść każdą z nierówności do kwadratu.
. Przy tym założeniu możemy podnieść każdą z nierówności do kwadratu.
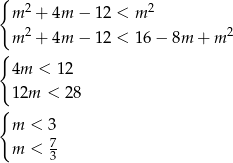
Mamy stąd 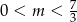 . W połączeniu z wcześniej wyliczonym warunkiem na
. W połączeniu z wcześniej wyliczonym warunkiem na 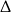 -ę, mamy więc
-ę, mamy więc
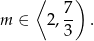
Odpowiedź: