/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom podstawowy 4 marca 2021 Czas pracy: 170 minut
Zadania zamknięte
Liczba 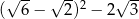 jest równa
jest równa
A) 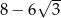 B)
B) 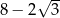 C)
C) 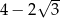 D)
D) 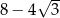
Liczba 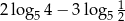 jest równa
jest równa
A) 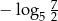 B)
B) 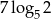 C)
C) 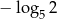 D)
D) 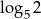
Medyczna maseczka ochronna wielokrotnego użytku z wymiennymi filtrami wskutek podwyżki zdrożała o 40% i kosztuje obecnie 106,40 zł. Cena maseczki przed podwyżką była równa
A) 63,84 zł B) 65,40 zł C) 76,00 zł D) 66,40 zł
Dla każdej dodatniej liczby 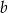 wyrażenie
wyrażenie 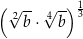 jest równe
jest równe
A) 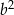 B)
B) 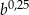 C)
C) 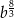 D)
D) 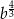
Para liczb 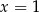 ,
, 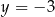 spełnia układ równań
spełnia układ równań
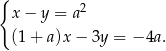
Wtedy  jest równe
jest równe
A) 2 B) 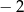 C)
C) 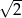 D)
D) 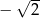
Iloczyn wszystkich rozwiązań równania 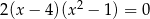 jest równy
jest równy
A) 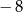 B)
B) 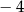 C) 4 D) 8
C) 4 D) 8
Zbiorem rozwiązań nierówności 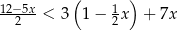 jest
jest
A) 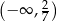 B)
B) 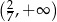 C)
C) 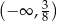 D)
D) 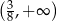
Funkcja liniowa 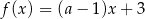 osiąga wartość najmniejszą równą 3. Wtedy
osiąga wartość najmniejszą równą 3. Wtedy
A) 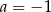 B)
B) 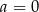 C)
C) 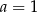 D)
D) 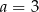
Na wykresie przedstawiono wykres funkcji 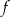 .
.
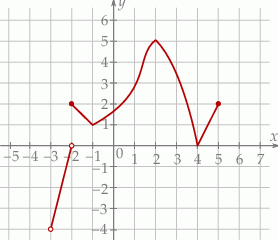
Wskaż zdanie prawdziwe.
A) Dziedziną funkcji 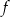 jest przedział
jest przedział 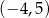 .
.
B) Funkcja 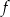 ma dwa miejsca zerowe.
ma dwa miejsca zerowe.
C) Funkcja 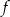 dla argumentu 1 przyjmuje wartość
dla argumentu 1 przyjmuje wartość 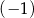 .
.
D) Zbiorem wartości funkcji 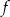 jest przedział
jest przedział ![(− 4,5]](https://img.zadania.info/zes/0066137/HzesT44x.gif) .
.
Funkcja 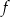 jest określona wzorem
jest określona wzorem 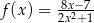 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wartość funkcji
. Wartość funkcji 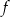 dla argumentu 1 jest równa
dla argumentu 1 jest równa
A) 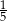 B)
B) 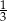 C) 1 D) 2
C) 1 D) 2
Ciąg 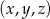 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że 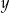 jest równe
jest równe
A) 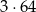 B)
B) 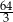 C) 4 D) 3
C) 4 D) 3
Ciąg 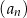 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 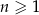 , jest arytmetyczny. Różnica tego ciągu jest równa 5, a pierwszy wyraz tego ciągu jest równy
, jest arytmetyczny. Różnica tego ciągu jest równa 5, a pierwszy wyraz tego ciągu jest równy 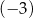 . Wtedy iloraz
. Wtedy iloraz 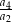 jest równy
jest równy
A)  B) 2 C) 6 D) 25
B) 2 C) 6 D) 25
Trójkąt 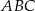 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 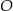 . Miara kąta
. Miara kąta 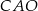 jest równa
jest równa 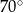 (zobacz rysunek).
(zobacz rysunek).
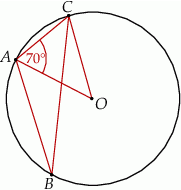
Wtedy miara kąta 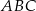 jest równa
jest równa
A) 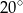 B)
B) 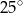 C)
C) 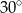 D)
D) 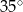
Ciągi 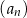 ,
, 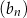 oraz
oraz 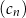 są określone dla każdej liczby naturalnej
są określone dla każdej liczby naturalnej 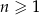 następująco:
następująco:
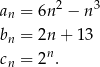
Wskaż zdanie prawdziwe.
A) Ciąg 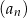 jest arytmetyczny.
jest arytmetyczny.
B) Ciąg 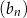 jest arytmetyczny.
jest arytmetyczny.
C) Ciąg 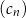 jest arytmetyczny.
jest arytmetyczny.
D) Wśród ciągów 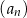 ,
, 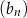 ,
, 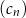 nie ma ciągu arytmetycznego.
nie ma ciągu arytmetycznego.
Ciąg 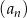 jest określony wzorem
jest określony wzorem 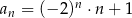 dla każdej liczby naturalnej
dla każdej liczby naturalnej 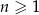 . Wtedy trzeci wyraz tego ciągu jest równy
. Wtedy trzeci wyraz tego ciągu jest równy
A) 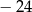 B)
B) 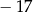 C)
C) 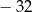 D)
D) 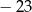
W romb o boku 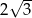 i kącie
i kącie 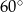 wpisano okrąg. Promień tego okręgu jest równy
wpisano okrąg. Promień tego okręgu jest równy
A) 3 B) 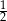 C)
C)  D)
D) 
Przez punkt przecięcia wysokości trójkąta równobocznego 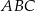 poprowadzono prostą
poprowadzono prostą 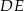 równoległą do podstawy
równoległą do podstawy 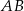 (zobacz rysunek).
(zobacz rysunek).
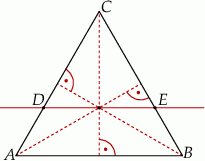
Stosunek pola trójkąta 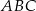 do pola trójkąta
do pola trójkąta 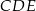 jest równy
jest równy
A) 9 : 4 B) 4 : 1 C) 4 : 9 D) 3 : 2
Końcami odcinka 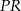 są punkty
są punkty 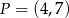 i
i 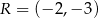 . Odległość punktu
. Odległość punktu 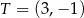 od środka odcinka
od środka odcinka 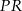 jest równa
jest równa
A) 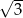 B)
B) 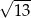 C)
C) 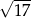 D)
D) 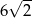
Kąt  jest ostry oraz
jest ostry oraz 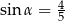 . Wtedy
. Wtedy
A) 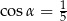 B)
B) 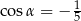 C)
C) 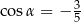 D)
D) 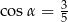
Dane są punkty 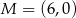 ,
, 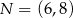 oraz
oraz 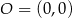 . Tangens kąta ostrego
. Tangens kąta ostrego 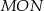 jest równy
jest równy
A) 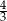 B)
B) 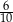 C)
C)  D)
D) 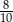
Proste o równaniach 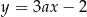 i
i 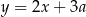 są prostopadłe. Wtedy
są prostopadłe. Wtedy  jest równe
jest równe
A)  B)
B) 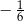 C)
C)  D)
D) 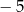
Dany jest trapez 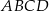 , w którym boki
, w którym boki 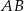 i
i 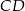 są równoległe oraz
są równoległe oraz 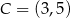 . Wierzchołki
. Wierzchołki 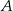 i
i 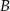 tego trapezu leżą na prostej o równaniu
tego trapezu leżą na prostej o równaniu 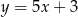 . Wtedy bok
. Wtedy bok 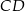 tego trapezu zawiera się w prostej o równaniu
tego trapezu zawiera się w prostej o równaniu
A) 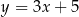 B)
B) 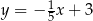 C)
C) 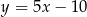 D)
D) 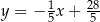
W trapezie równoramiennym 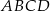 podstawy
podstawy 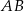 i
i 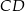 mają długości równe odpowiednio
mają długości równe odpowiednio  i
i 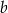 (przy czym
(przy czym 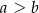 ). Miara kąta ostrego trapezu jest równa
). Miara kąta ostrego trapezu jest równa 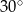 . Wtedy wysokość tego trapezu jest równa
. Wtedy wysokość tego trapezu jest równa
A) 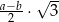 B)
B) 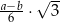 C)
C) 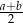 D)
D) 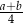
Przekątna sześcianu ma długość 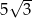 . Wtedy objętość tego sześcianu jest równa
. Wtedy objętość tego sześcianu jest równa
A) 125 B) 75 C) 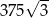 D)
D) 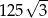
Ostrosłupy prawidłowe trójkątne 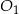 i
i 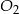 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 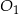 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 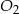 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 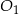 do objętości ostrosłupa
do objętości ostrosłupa 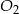 jest równy
jest równy
A) 3 : 1 B) 1 : 3 C) 9 : 1 D) 1 : 9
Wszystkich liczb naturalnych trzycyfrowych parzystych, w których cyfra 7 występuje dokładnie jeden raz, jest
A) 85 B) 90 C) 100 D) 150
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 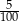 C)
C) 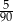 D)
D) 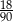
Liczba  jest dodatnia. Mediana zestawu czterech liczb:
jest dodatnia. Mediana zestawu czterech liczb: 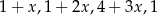 , jest równa 10. Wtedy
, jest równa 10. Wtedy
A) 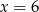 B)
B) 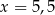 C)
C) 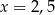 D)
D) 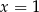
Zadania otwarte
Rozwiąż nierówność:
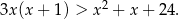
Rozwiąż równanie
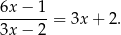
Dany jest trójkąt prostokątny, którego przyprostokątne mają długości  i
i 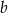 . Punkt
. Punkt 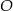 leży na przeciwprostokątnej tego trójkąta i jest środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek).
leży na przeciwprostokątnej tego trójkąta i jest środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek).
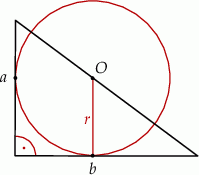
Wykaż, że promień  tego okręgu jest równy
tego okręgu jest równy 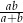 .
.
Kąt  jest ostry i
jest ostry i 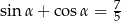 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 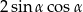 .
.
Dany jest czworokąt 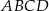 , w którym
, w którym 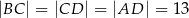 .
.
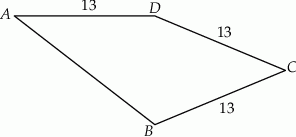
Przekątna 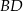 tego czworokąta ma długość 10 i jest prostopadła do boku
tego czworokąta ma długość 10 i jest prostopadła do boku 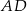 . Oblicz pole czworokąta
. Oblicz pole czworokąta 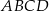 .
.
Funkcja kwadratowa 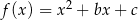 nie ma miejsc zerowych. Wykaż, że
nie ma miejsc zerowych. Wykaż, że 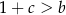 .
.
Rosnący ciąg arytmetyczny 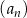 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 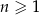 . Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy
. Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy 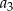 ,
, 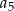 ,
, 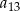 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego 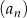 .
.

