/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 30 kwietnia 2016 Czas pracy: 180 minut
Zadania zamknięte
Dany jest nieskończony ciąg geometryczny 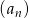 określony wzorem
określony wzorem 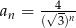 dla
dla 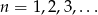 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A) 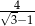 B)
B) 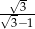 C)
C) 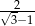 D)
D) 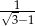
Funkcja 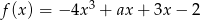 jest funkcją malejąca jeżeli
jest funkcją malejąca jeżeli
A) 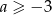 B)
B) 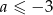 C)
C) 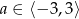 D)
D) 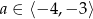
Wskaż wartość parametru 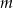 , dla którego prosta
, dla którego prosta 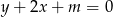 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 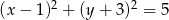
A) 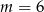 B)
B) 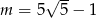 C)
C) 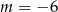 D)
D) 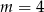
Wielomian 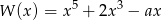 jest podzielny przez wielomian
jest podzielny przez wielomian 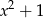 . Wynika stąd, że
. Wynika stąd, że
A) 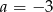 B)
B) 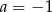 C)
C) 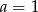 D)
D) 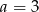
Niech 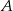 i
i 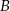 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 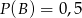 i
i 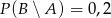 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 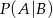 jest równe
jest równe
A) 0,3 B) 0,6 C) 0,5 D) 0,18
Zadania otwarte
Funkcja 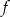 jest określona wzorem
jest określona wzorem 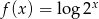 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 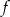 w punkcie
w punkcie 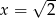
Oblicz granicę 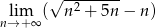 .
.
Dana jest parabola o równaniu 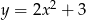 i leżący na niej punkt
i leżący na niej punkt 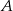 o współrzędnej
o współrzędnej  równej
równej 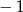 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 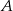 .
.
Długości boków trójkąta 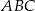 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 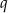 . Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta
. Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta 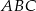 są równe miarom kątów trójkąta
są równe miarom kątów trójkąta 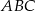 .
.
Wierzchołki 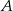 i
i 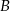 kwadratu
kwadratu 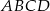 leżą na paraboli
leżą na paraboli 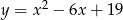 , przy czym odcinek
, przy czym odcinek 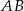 jest równoległy do osi
jest równoległy do osi 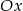 . Wykaż, że jeżeli odległość punktu
. Wykaż, że jeżeli odległość punktu 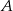 od osi
od osi 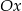 jest liczbą całkowitą to pole kwadratu
jest liczbą całkowitą to pole kwadratu 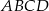 również jest liczbą całkowitą.
również jest liczbą całkowitą.
Wyznacz dziedzinę funkcji 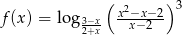
Przez środek okręgu wpisanego w trójkąt równoboczny 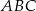 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 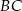 i przecinającą bok
i przecinającą bok 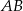 w punkcie
w punkcie 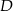 . Oblicz iloraz
. Oblicz iloraz 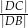 .
.
Rozwiąż równanie 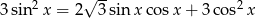 w przedziale
w przedziale 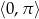 .
.
Wykres funkcji homograficznej 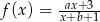 można otrzymać przesuwając wykres funkcji
można otrzymać przesuwając wykres funkcji 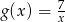 , a dziedzina funkcji
, a dziedzina funkcji 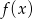 jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki
jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki  i
i 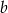 .
.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 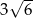 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
, a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
Suma długości wszystkich krawędzi prostopadłościanu jest równa 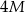 , a jedna z jego ścian na pole powierzchni trzy razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
, a jedna z jego ścian na pole powierzchni trzy razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.

