/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 27 kwietnia 2019 Czas pracy: 180 minut
Zadania zamknięte
Liczba 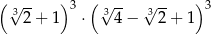 jest równa
jest równa
A) 1 B) 8 C) 27 D) 64
Równanie 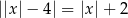
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie cztery rozwiązania.
Wyrażenie 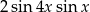 jest równe
jest równe
A) 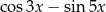 B)
B) 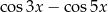 C)
C) 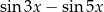 D)
D) 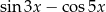
Na rysunku zaznaczono zbiór punktów płaszczyzny spełniających układ nierówności:
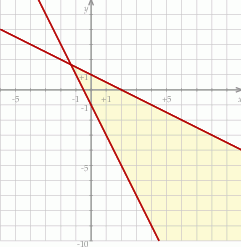
A) 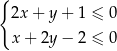 B)
B) 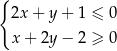
C) 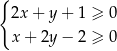 D)
D) 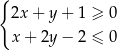
Granica 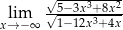
A) nie istnieje. B) jest liczbą dodatnią.
C) jest liczbą ujemną. D) jest równa 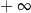 .
.
Zadania otwarte
Punkt 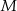 przyprostokątnej
przyprostokątnej 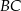 trójkąta prostokątnego
trójkąta prostokątnego 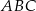 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 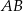 otrzymując punkt
otrzymując punkt 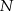 . Wykaż, że
. Wykaż, że 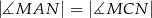 .
.
Dany jest nieskończony ciąg okręgów 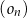 o równaniach
o równaniach 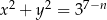 ,
, 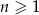 . Niech
. Niech 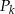 będzie pierścieniem ograniczonym zewnętrznym okręgiem
będzie pierścieniem ograniczonym zewnętrznym okręgiem 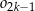 i wewnętrznym okręgiem
i wewnętrznym okręgiem 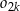 . Oblicz sumę pól wszystkich pierścieni
. Oblicz sumę pól wszystkich pierścieni 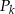 , gdzie
, gdzie 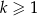 .
.
Udowodnij, że jeżeli 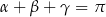 , to
, to
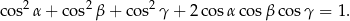
Rozpatrujemy wszystkie liczby naturalne dziewięciocyfrowe, w zapisie których mogą występować wyłącznie cyfry 0, 1, 2 przy czym każda z cyfr występuje dokładnie trzy razy. Ile jest takich liczb?
Liczby 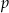 i
i 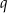 są pierwiastkami równania
są pierwiastkami równania 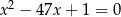 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 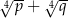 jest liczbą naturalną.
jest liczbą naturalną.
W pudełku znajdują się klocki o różnych kształtach i kolorach. Wiadomo, że prawdopodobieństwo wylosowania klocka, który ma kształt walca lub ma kolor czerwony jest równe 0,6. Prawdopodobieństwo, że losowo wybrany klocek czerwony jest walcem jest równe 0,25. Wiadomo też, że klocki czerwone stanowią 40% wszystkich klocków. Jakie jest prawdopodobieństwo, że losowo wybrany klocek w kształcie walca jest czerwony?
W trójkącie 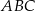 długości boków
długości boków 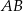 i
i 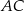 są odpowiednio równe 4 i 6. Punkt
są odpowiednio równe 4 i 6. Punkt 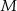 jest środkiem odcinka
jest środkiem odcinka 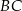 , a długość środkowej
, a długość środkowej 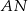 trójkąta
trójkąta 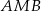 jest równa 3. Oblicz długość boku
jest równa 3. Oblicz długość boku 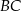 .
.
Dany jest malejący ciąg geometryczny 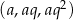 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi niepodzielnymi przez 3. Jeśli najmniejszy wyraz ciągu zwiększymy o 18, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi niepodzielnymi przez 3. Jeśli najmniejszy wyraz ciągu zwiększymy o 18, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 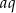 tego ciągu.
tego ciągu.
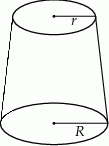
Przedstawiona na rysunku bryła to stożek ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 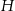 , a
, a  i
i 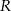 (
(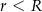 ) są promieniami podstaw. Oblicz objętość tej bryły.
) są promieniami podstaw. Oblicz objętość tej bryły.
Funkcja 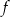 jest wielomianem stopnia 3, a jej wykres jest styczny do prostej
jest wielomianem stopnia 3, a jej wykres jest styczny do prostej 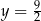 w punkcie o odciętej
w punkcie o odciętej 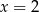 oraz jest styczny do prostej
oraz jest styczny do prostej 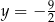 w punkcie o odciętej
w punkcie o odciętej 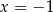 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 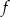 .
.
Z punktu 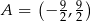 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 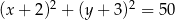 . Oblicz pole trójkąta
. Oblicz pole trójkąta 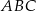 , gdzie
, gdzie 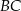 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Rozpatrujemy wszystkie graniastosłupy prawidłowe czworokątne o polu powierzchni całkowitej 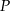 . Wyznacz wysokość i długość krawędzi podstawy tego graniastosłupa, którego objętość jest największa. Oblicz tę największą objętość.
. Wyznacz wysokość i długość krawędzi podstawy tego graniastosłupa, którego objętość jest największa. Oblicz tę największą objętość.

