/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 22 kwietnia 2023 Czas pracy: 180 minut
Rozwiąż równanie 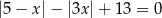 .
.
Dany jest nieskończony ciąg geometryczny 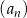 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 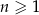 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 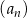 jest równa 26, a suma
jest równa 26, a suma 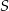 wszystkich wyrazów tego ciągu jest równa 27. Wyznacz wszystkie wartości
wszystkich wyrazów tego ciągu jest równa 27. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
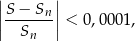
gdzie 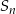 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 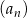 .
.
Informacja do zadań 3.1 i 3.2
Dana jest funkcja kwadratowa 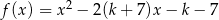 określona dla dowolnego
określona dla dowolnego 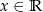 .
.
Wykaż, że jeżeli funkcja 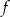 ma dwa różne miejsca zerowe:
ma dwa różne miejsca zerowe: 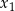 i
i 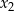 , to miejscami zerowymi funkcji
, to miejscami zerowymi funkcji 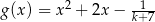 , określonej dla
, określonej dla 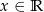 , są liczby
, są liczby 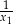 i
i 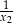 .
.
Wyznacz wszystkie wartości parametru 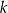 , dla których funkcja
, dla których funkcja 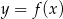 ma dwa różne miejsca zerowe należące do przedziału
ma dwa różne miejsca zerowe należące do przedziału 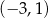 .
.
Oblicz granicę
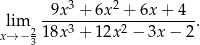
Dany jest wielomian 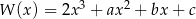 . Rozwiązaniem nierówności
. Rozwiązaniem nierówności 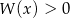 jest zbiór
jest zbiór 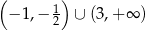 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 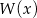 przez dwumian
przez dwumian 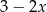 .
.
Linia produkcyjna w fabryce elektroniki wytwarza jeden rodzaj kart graficznych. Aby produkcja była opłacalna, dzienna wielkość produkcji musi wynosić co najmniej 576 kart i nie może przekroczyć 620 kart (ze względu na ograniczone moce produkcyjne). Przy poziomie produkcji 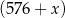 kart graficznych dziennie przeciętny koszt
kart graficznych dziennie przeciętny koszt 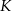 (w złotych) wytworzenia jednej karty jest równy
(w złotych) wytworzenia jednej karty jest równy
![2 3x2 − 103,5x + 42 4764 K (x) = ------------------------, gdzie x ∈ [0,44] 576+ x](https://img.zadania.info/zes/0069624/HzesT30x.gif)
Oblicz, ile kart graficznych powinna wytwarzać dziennie ta linia produkcyjna, aby przeciętny koszt produkcji jednej karty był najmniejszy (z zachowaniem opłacalności produkcji). Oblicz ten najmniejszy przeciętny koszt.
Rozwiąż równanie
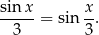
Proste zawierające wysokości trójkąta ostrokątnego 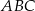 przecinają boki
przecinają boki 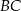 ,
, 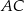 i
i 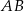 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 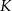 ,
, 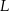 i
i 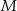 . Wykaż, że jeżeli trójkąt
. Wykaż, że jeżeli trójkąt 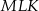 jest podobny do trójkąta
jest podobny do trójkąta 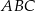 , to trójkąt
, to trójkąt 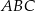 jest równoboczny.
jest równoboczny.
Podstawą graniastosłupa prostego 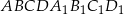 jest trapez równoramienny
jest trapez równoramienny 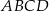 wpisany w okrąg o środku
wpisany w okrąg o środku 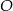 i promieniu
i promieniu 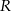 . Dłuższa podstawa
. Dłuższa podstawa 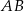 trapezu jest średnicą tego okręgu, a krótsza ma długość
trapezu jest średnicą tego okręgu, a krótsza ma długość  (zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
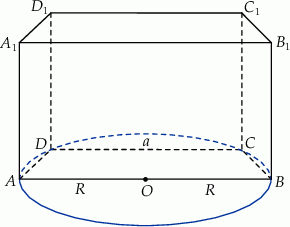
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 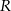 , długości podstawy
, długości podstawy  i miary kąta
i miary kąta  .
.
Punkt  jest wierzchołkiem rozwartokątnego trójkąta równoramiennego
jest wierzchołkiem rozwartokątnego trójkąta równoramiennego  , w którym
, w którym 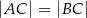 . Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok
. Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok 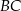 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 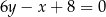 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 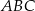 .
.
Pracownik parkingu zanotował numery rejestracyjne piętnastu kolejnych samochodów, które wjechały na parking. Oblicz prawdopodobieństwo, że wśród tych piętnastu numerów rejestracyjnych co najwyżej 3 nie kończyły się cyfrą 7. Przyjmij, że każdy z numerów rejestracyjnych był zakończony cyfrą, i że wystąpienie każdej z dziesięciu cyfr na końcu numeru rejestracyjnego jest jednakowo prawdopodobne.

