/Szkoła średnia

Egzamin Maturalny
z Matematyki poziom rozszerzony 9 maja 2014 Czas pracy: 170 minut

Zadanie 1
(4 pkt)

Dana jest funkcja 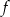f określona wzorem 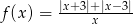f(x) = |x+-3|+|x−3|- x dla każdej liczby rzeczywistej 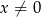x ⁄= 0 . Wyznacz zbiór wartości tej funkcji.

Zadanie 2
(6 pkt)

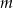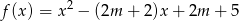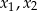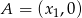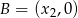Wyznacz wszystkie wartości parametru m , dla których funkcja kwadratowa f (x) = x2 − (2m + 2)x + 2m + 5 ma dwa różne pierwiastki x 1,x2 takie, że suma kwadratów odległości punktów A = (x1,0) i B = (x2,0) od prostej o równaniu 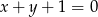x+ y+ 1 = 0 jest równa 6.

Zadanie 3
(4 pkt)

Rozwiąż równanie 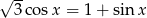√ -- 3 cosx = 1+ sin x w przedziale ⟨0,2π ⟩ .

Zadanie 4
(3 pkt)

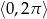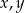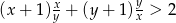Udowodnij, że dla każdych dwóch liczb rzeczywistych dodatnich x ,y prawdziwa jest nierówność (x + 1)x + (y + 1) y> 2 y x .

Zadanie 5
(5 pkt)

Dane są trzy okręgi o środkach 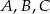A ,B,C i promieniach równych odpowiednio 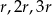r,2r,3r . Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie 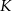K , drugi z trzecim w punkcie 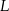L i trzeci z pierwszym w punkcie 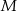M . Oblicz stosunek pola trójkąta 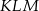KLM do pola trójkąta ABC .

Zadanie 6
(3 pkt)

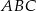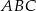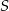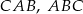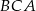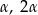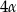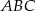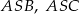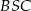Trójkąt ABC jest wpisany w okrąg o środku S . Kąty wewnętrzne CAB , ABC i BCA tego trójkąta są równe, odpowiednio, α , 2α i 4α . Wykaż, że trójkąt ABC jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych ASB , ASC i BSC tworzą w podanej kolejności ciąg arytmetyczny.

Zadanie 7
(6 pkt)

Ciąg geometryczny 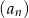(an) ma 100 wyrazów i są one liczbami dodatnimi. Suma wszystkich wyrazów o numerach nieparzystych jest sto razy większa od sumy wszystkich wyrazów o numerach parzystych oraz

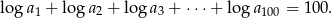
log a1 + lo ga2 + log a3 + ⋅ ⋅⋅+ log a100 = 100.

Oblicz 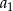a1 .

Zadanie 8
(4 pkt)

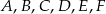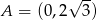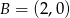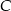Punkty A ,B ,C ,D ,E ,F są kolejnymi wierzchołkami sześciokąta foremnego, przy czym √ -- A = (0,2 3) , B = (2,0) , a C leży na osi 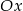Ox . Wyznacz równanie stycznej do okręgu opisanego na tym sześciokącie przechodzącej przez wierzchołek E .

Zadanie 9
(6 pkt)

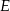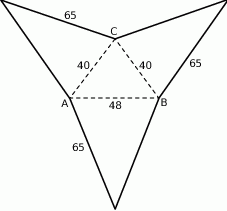
Oblicz objętość ostrosłupa trójkątnego 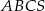ABCS , którego siatkę przedstawiono na rysunku.

PIC

Zadanie 10
(5 pkt)

Wyznacz wszystkie całkowite wartości parametru 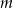m , dla których równanie

3 2 [ 2 2 ] (x + 2x + 2x + 1 ) x − (2m + 1)x + m + m = 0

ma trzy, parami różne, pierwiastki rzeczywiste, takie że jeden z nich jest średnią arytmetyczną dwóch pozostałych.

Zadanie 11
(4 pkt)

Z urny zawierającej 10 kul ponumerowanych kolejnymi liczbami od 1 do 10 losujemy jednocześnie trzy kule. Oblicz prawdopodobieństwo zdarzenia 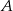A polegającego na tym, że numer jednej z wylosowanych kul jest równy sumie numerów dwóch pozostałych kul.

Arkusz Wersja PDF
Rozwiązania