/Szkoła średnia
Egzamin Maturalny
z Matematyki (termin dodatkowy)
formuła 2015
poziom podstawowy 2 czerwca 2023 Czas pracy: 170 minut
Zadania zamknięte
Liczba 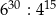 jest równa
jest równa
A) 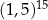 B)
B) 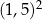 C)
C) 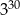 D)
D) 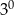
Dla każdej dodatniej liczby rzeczywistej  iloczyn
iloczyn 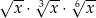 jest równy
jest równy
A)  B)
B) 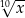 C)
C) 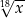 D)
D) 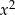
Klient wpłacił do banku 30 000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości 7% od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania łączna wartość doliczonych odsetek na tej lokacie (bez uwzględniania podatków) jest równa
A) 2100 zł B) 2247 zł C) 4200 zł D) 4347 zł
Liczba 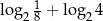 jest równa
jest równa
A) 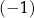 B)
B) 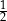 C) 2 D) 5
C) 2 D) 5
Liczba 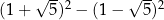 jest równa
jest równa
A) 0 B) 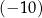 C)
C) 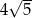 D)
D) 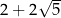
Do zbioru rozwiązań nierówności 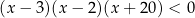 należy liczba
należy liczba
A) 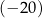 B)
B) 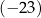 C) 20 D) 23
C) 20 D) 23
Informacja do zadań 7 i 8
Na rysunku przedstawiono wykres funkcji 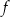 .
.
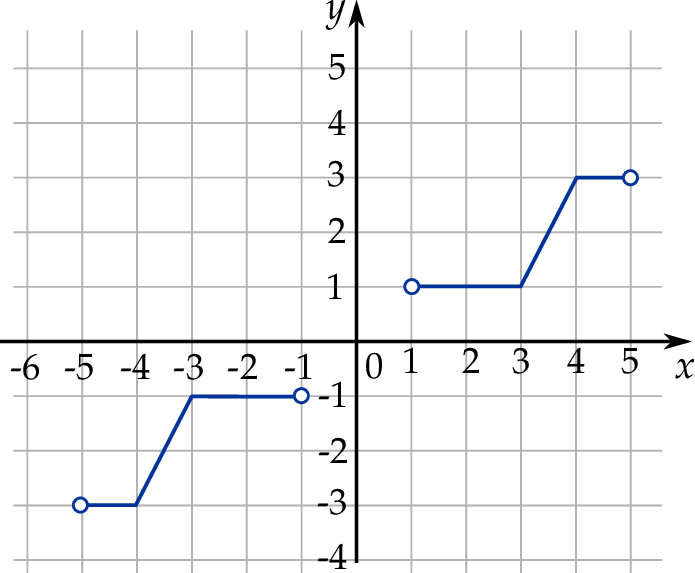
Dziedziną funkcji 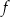 jest zbiór
jest zbiór
A) 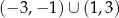 B)
B) 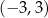 C)
C) 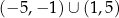 D)
D) 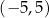
Zbiorem wartości funkcji 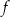 jest zbiór
jest zbiór
A) 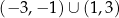 B)
B) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zes/0070898/HzesT30x.png)
C) 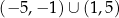 D)
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zes/0070898/HzesT32x.png)
Funkcja 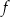 jest określona wzorem
jest określona wzorem 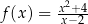 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 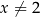 . Wartość funkcji
. Wartość funkcji 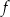 dla argumentu 4 jest równa
dla argumentu 4 jest równa
A) 6 B) 2 C) 10 D) 8
W kartezjańskim układzie współrzędnych 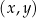 prosta o równaniu
prosta o równaniu 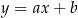 przechodzi przez punkty
przechodzi przez punkty 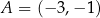 oraz
oraz 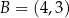 . Współczynnik
. Współczynnik  w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 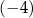 B)
B) 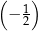 C) 2 D)
C) 2 D) 
W kartezjańskim układzie współrzędnych 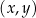 wykresy funkcji liniowych
wykresy funkcji liniowych 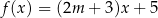 oraz
oraz 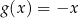 nie mają punktów wspólnych dla
nie mają punktów wspólnych dla
A) 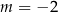 B)
B) 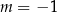 C)
C) 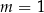 D)
D) 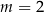
Funkcja kwadratowa 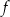 jest określona wzorem
jest określona wzorem 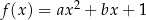 , gdzie
, gdzie  oraz
oraz 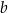 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 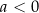 i
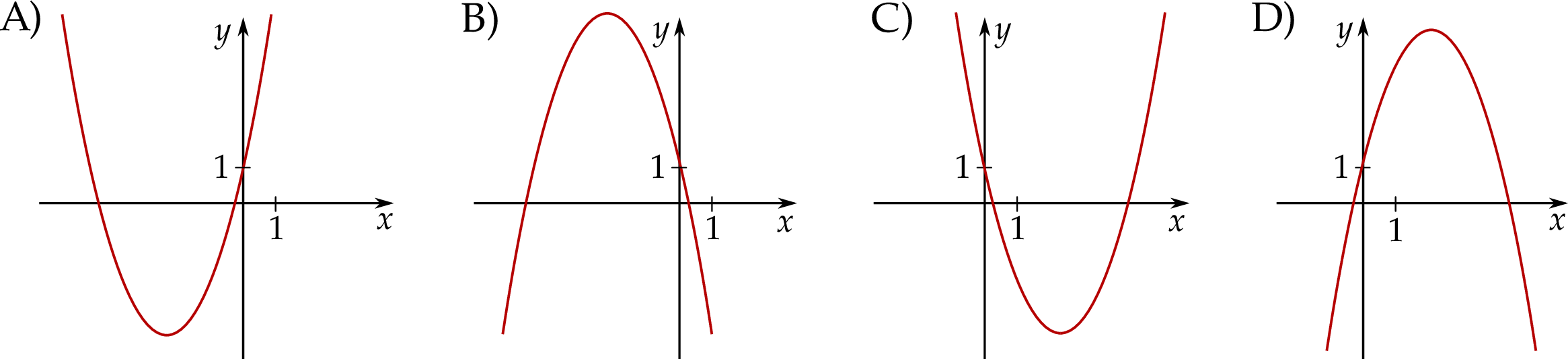
i 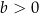 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 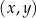 . Fragment wykresu funkcji
. Fragment wykresu funkcji 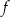 przedstawiono na rysunku
przedstawiono na rysunku
Ciąg 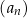 jest określony wzorem
jest określony wzorem 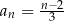 dla każdej liczby naturalnej
dla każdej liczby naturalnej 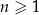 . Liczba wyrazów tego ciągu mniejszych od 10 jest równa
. Liczba wyrazów tego ciągu mniejszych od 10 jest równa
A) 28 B) 31 C) 32 D) 27
Ciąg 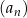 , określony wzorem
, określony wzorem 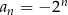 dla każdej liczby naturalnej
dla każdej liczby naturalnej 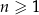 , jest
, jest
A) ciągiem arytmetycznym o różnicy 2.
B) ciągiem arytmetycznym o różnicy 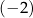 .
.
C) ciągiem geometrycznym o ilorazie 2.
D) ciągiem geometrycznym o ilorazie 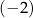 .
.
Trzywyrazowy ciąg 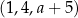 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba  jest równa
jest równa
A) 0 B) 7 C) 2 D) 11
Ciąg geometryczny 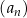 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 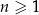 . W tym ciągu
. W tym ciągu 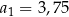 oraz
oraz 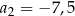 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 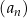 jest równa
jest równa
A) 11,25 B) 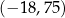 C) 15 D)
C) 15 D) 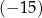
Dla każdego kąta ostrego  wyrażenie
wyrażenie 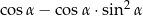 jest równe
jest równe
A) 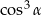 B)
B) 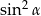 C)
C) 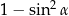 D)
D) 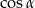
Cosinus kąta ostrego  jest równy
jest równy  . Wtedy
. Wtedy 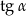 jest równy
jest równy
A) 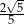 B)
B) 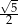 C) 2 D)
C) 2 D) 
Na łukach 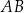 i
i 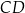 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 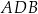 i
i 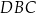 , takie, że
, takie, że 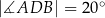 i
i 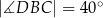 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 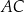 i
i 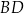 przecinają się w punkcie
przecinają się w punkcie 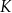 .
.

Miara kąta 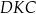 jest równa
jest równa
A) 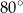 B)
B) 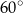 C)
C) 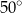 D)
D) 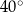
Pole równoległoboku 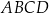 jest równe
jest równe 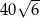 . Bok
. Bok 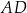 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 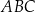 równoległoboku ma miarę
równoległoboku ma miarę 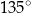 (zobacz rysunek).
(zobacz rysunek).

Długość boku 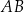 jest równa
jest równa
A) 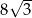 B)
B) 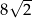 C)
C) 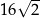 D)
D) 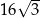
Odcinek 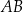 jest średnicą okręgu o środku
jest średnicą okręgu o środku 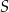 . Prosta
. Prosta 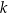 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 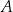 . Prosta
. Prosta 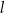 przecina ten okrąg w punktach
przecina ten okrąg w punktach 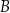 i
i 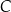 . Proste
. Proste 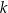 i
i 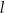 przecinają się w punkcie
przecinają się w punkcie 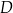 , przy czym
, przy czym 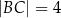 i
i 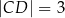 (zobacz rysunek).
(zobacz rysunek).

Odległość punktu 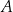 od prostej
od prostej 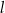 jest równa
jest równa
A) 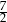 B) 5 C)
B) 5 C) 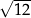 D)
D) 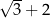
Funkcja liniowa 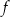 jest określona wzorem
jest określona wzorem 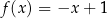 . Funkcja
. Funkcja 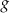 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 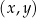 wykres funkcji
wykres funkcji 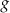 przechodzi przez punkt
przechodzi przez punkt 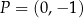 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 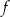 . Wzorem funkcji
. Wzorem funkcji 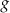 jest
jest
A) 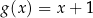 B)
B) 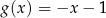 C)
C) 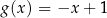 D)
D) 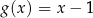
W kartezjańskim układzie współrzędnych 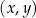 dane są punkty
dane są punkty 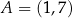 oraz
oraz 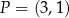 . Punkt
. Punkt 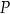 dzieli odcinek
dzieli odcinek 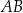 tak, że
tak, że 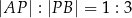 . Punkt
. Punkt 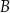 ma współrzędne
ma współrzędne
A) 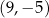 B)
B) 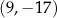 C)
C) 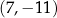 D)
D) 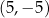
W kartezjańskim układzie współrzędnych 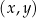 punkty
punkty 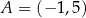 oraz
oraz 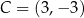 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 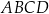 . Pole kwadratu
. Pole kwadratu 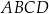 jest równe
jest równe
A) 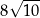 B)
B) 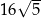 C) 40 D) 80
C) 40 D) 80
Punkt 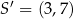 jest obrazem punktu
jest obrazem punktu 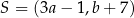 w symetrii osiowej względem osi
w symetrii osiowej względem osi 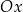 układu współrzędnych, gdy
układu współrzędnych, gdy
A) 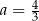 oraz
oraz 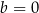 B)
B) 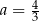 oraz
oraz 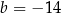
C) 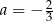 oraz
oraz 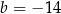 D)
D) 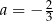 oraz
oraz 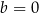
Objętość ostrosłupa prawidłowego trójkątnego o wysokości 8 jest równa 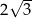 . Długość krawędzi podstawy tego ostrosłupa jest równa
. Długość krawędzi podstawy tego ostrosłupa jest równa
A) 3 B) 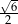 C) 1 D)
C) 1 D) 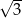
Dany jest graniastosłup prawidłowy sześciokątny 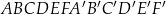 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 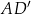 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 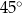 (zobacz rysunek).
(zobacz rysunek).
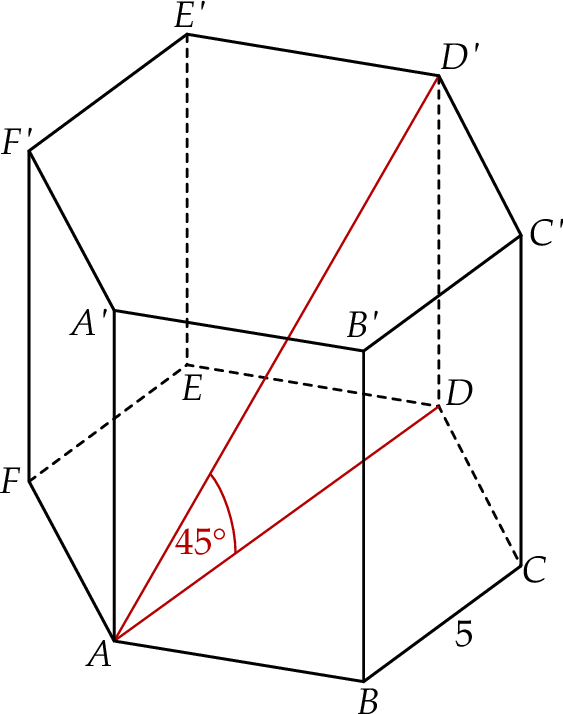
Pole ściany bocznej tego graniastosłupa jest równe
A) 12,5 B) 25 C) 50 D) 100
Średnia arytmetyczna zestawu pewnych stu liczb całkowitych dodatnich jest równa  . Każdą z liczb tego zestawu zwiększamy o 4, w wyniku czego otrzymujemy nowy zestaw stu liczb. Średnia arytmetyczna nowego zestawu stu liczb jest równa
. Każdą z liczb tego zestawu zwiększamy o 4, w wyniku czego otrzymujemy nowy zestaw stu liczb. Średnia arytmetyczna nowego zestawu stu liczb jest równa
A) 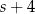 B)
B) 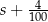 C)
C) 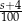 D)
D) 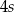
Wszystkich liczb naturalnych trzycyfrowych o sumie cyfr równej 3 jest
A) 8 B) 4 C) 5 D) 6
Zadania otwarte
Rozwiąż nierówność 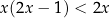 .
.
Rozwiąż równanie 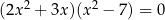 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 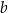 takiej, że
takiej, że 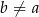 , prawdziwa jest nierówność
, prawdziwa jest nierówność
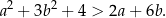
Wykresem funkcji kwadratowej 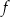 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 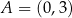 . Punkt
. Punkt 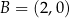 leży na wykresie funkcji
leży na wykresie funkcji 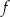 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 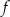 .
.
W trójkącie prostokątnym równoramiennym 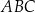 o przeciwprostokątnej
o przeciwprostokątnej 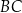 punkt
punkt 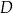 jest środkiem ramienia
jest środkiem ramienia 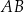 . Odcinek
. Odcinek 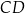 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
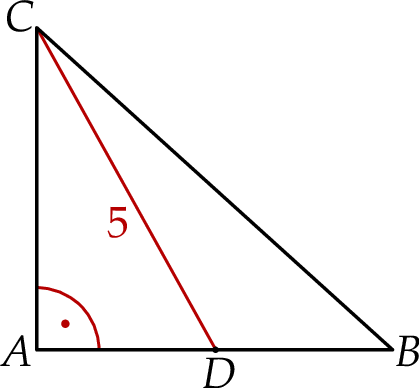
Oblicz obwód trójkąta 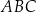 .
.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 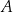 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia 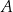 .
.
W trapezie równoramiennym 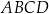 podstawa
podstawa 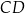 ma długość 5. Punkt
ma długość 5. Punkt 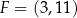 jest środkiem odcinka
jest środkiem odcinka 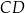 . Prosta o równaniu
. Prosta o równaniu 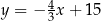 jest osią symetrii tego trapezu oraz
jest osią symetrii tego trapezu oraz 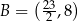 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka  oraz pole tego trapezu.
oraz pole tego trapezu.

