/Szkoła średnia

Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom rozszerzony 2 czerwca 2016 Czas pracy: 180 minut

Zadania zamknięte

Zadanie 1
(1 pkt)

Najprostszą postacią wyrażenia 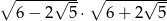∘ -----√--- ∘ -----√--- 6− 2 5 ⋅ 6 + 2 5 jest równa
A) 4 B) 16 C) 1 D) 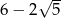√ -- 6 − 2 5

Zadanie 2
(1 pkt)

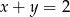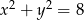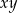Jeśli x+ y = 2 i x 2 + y2 = 8 , to xy równa się
A) 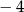− 4 B) 2 C) 4 D)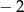 − 2

Zadanie 3
(1 pkt)

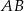Dla jakich wartości x odcinek AB jest równoległy do odcinka DE ?

PIC

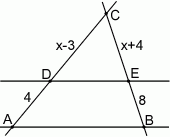
A) 12 B) 8 C) 6 D) 10

Zadania otwarte

Zadanie 4
(2 pkt)

Wysokość trójkąta równobocznego jest o 3 cm krótsza od długości jego boku. Oblicz promień okręgu opisanego na tym trójkącie.

Zadanie 5
(3 pkt)

Określ dziedzinę równania 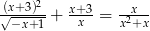(x+3)2- x+3- --x-- √−x-+1 + x = x2+x .

Zadanie 6
(3 pkt)

Sinus kąta ostrego jest dwa razy większy od cosinusa tego kąta. Wyznacz wartość cosinusa tego kąta i podaj przybliżoną wartość tego kąta.

Zadanie 7
(2 pkt)

Oblicz cosinus najmniejszego kąta α trójkąta o bokach 2 cm, 4 cm, 5 cm.

Zadanie 8
(3 pkt)

Wykaż, że suma kwadratów trzech liczb całkowitych, które przy dzieleniu przez 3 dają resztę 2 jest podzielna przez 3.

Zadanie 9
(5 pkt)

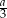Ze środka ciężkości trójkąta równobocznego o boku a , wykreślono okrąg o promieniu a3 . Oblicz pole części koła nie należącego do trójkąta.

Zadanie 10
(3 pkt)

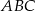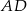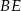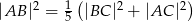W trójkącie ABC środkowe AD i BE są prostopadłe. Wykaż, że ( ) |AB |2 = 15 |BC |2 + |AC |2 .

Zadanie 11
(3 pkt)

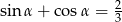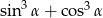Wiedząc, że sin α + cos α = 23 , oblicz sin 3α + cos3α .

Zadanie 12
(4 pkt)

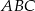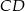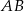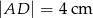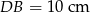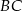W trójkącie ABC wysokość CD dzieli bok AB na odcinki długości |AD | = 4 cm i DB = 10 cm . Bok BC ma 16 cm długości. Poprowadzono symetralną boku 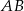AB . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok BC .

Zadanie 13
(4 pkt)

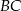Wykaż, że liczba 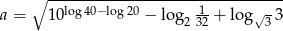--------------------------------- ∘ log40− log20 1- √ - a = 1 0 − lo g2 32 + log 33 jest liczbą naturalną.

Zadanie 14
(5 pkt)

Dane są zbiory: 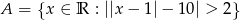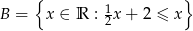A = {x ∈ R : ||x − 1|− 10| > 2} , { } B = x ∈ R : 1x + 2 ≤ x 2 . Wyznacz zbiór A ∖B .

Zadanie 15
(6 pkt)

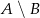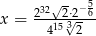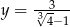Sprawdź, która liczba jest większa: 32√- − 5 x = 2---2√⋅23--6 415 2 , czy y = 3√-3-- 4− 1 .

Zadanie 16
(4 pkt)

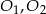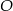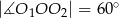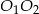Dane są okręgi o środkach O 1,O 2 oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku O i promieniu 5. Wiadomo, że |∡O 1OO 2| = 60∘ . Oblicz długość odcinka O 1O 2 .

Arkusz Wersja PDF
Rozwiązania