/Szkoła średnia

Zadanie nr 7547293

Dodaj do ulubionych
Dodaj do rozwiązanych

Grupa rowerzystów jechała ze stałą prędkością do miasta oddalonego o 120 km. Gdyby jechali ze średnią prędkością o 5 km/godz. większą, to przejechaliby tę odległość w czasie o 2 godziny krótszym. Wyznacz średnią prędkość grupy i czas przejazdu.

Rozwiązanie

Oznaczmy przez 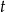t czas jaki potrzebowała grupa na przejechanie trasy oraz przez 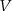V prędkość tej grupy. Z założeń możemy zapisać układ równań

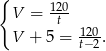
{ V = 120t- 120- V + 5 = t− 2.

Podstawiamy pierwsze równanie do drugiego i liczymy

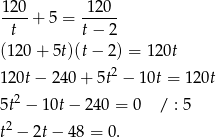
1 20 120 ---- + 5 = ----- t t − 2 (120 + 5t)(t − 2) = 12 0t 2 120t − 24 0+ 5t − 10t = 1 20t 5t2 − 10t− 240 = 0 / : 5 t2 − 2t− 48 = 0.

Liczymy pierwiastki

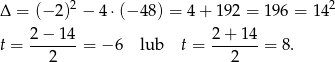
Δ = (− 2)2 − 4 ⋅(− 48) = 4+ 192 = 196 = 142 2 − 14 2 + 14 t = -------= − 6 lub t = -------= 8. 2 2

Odrzucamy wynik ujemny i otrzymujemy, że prędkość wynosiła

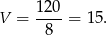
120 V = ----= 15. 8

 
Odpowiedź: 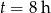t = 8 h i V = 15 km/h

Wersja PDF