/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 28 kwietnia 2018 Czas pracy: 170 minut
Zadania zamknięte
Niech 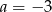 i
i 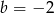 . Wartość wyrażenia
. Wartość wyrażenia 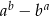 jest równa
jest równa
A) 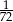 B)
B) 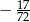 C)
C) 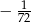 D)
D) 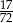
Liczba 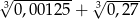 jest równa
jest równa
A) 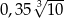 B) 0,35 C)
B) 0,35 C) 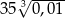 D) 3,5
D) 3,5
Stężenie roztworu początkowo wzrosło o 25%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 45% B) 50% C) 55% D) 60%
Liczba 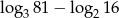 jest równa
jest równa
A) 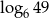 B)
B) 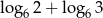 C)
C) 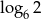 D)
D) 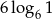
Liczba 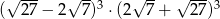 jest równa
jest równa
A) 1 B) 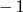 C)
C) 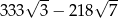 D)
D) 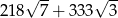
Do zbioru rozwiązań nierówności 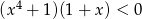 nie należy liczba
nie należy liczba
A) 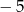 B)
B) 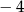 C)
C) 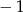 D)
D) 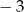
Funkcja liniowa 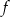 jest określona wzorem
jest określona wzorem 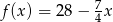 . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 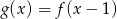 jest
jest
A) 17 B) 16 C) 15 D) 18
Rozwiązaniem równania 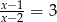 , gdzie
, gdzie 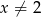 jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 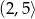 B)
B) 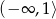 C)
C) 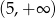 D)
D) 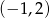
Pręt o długości 40 metrów rozcięto na trzy części, których długości pozostają w stosunku 4:5:6. Stąd wynika, że najkrótsza z tych części ma długość
A) 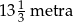 B)
B) 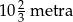 C)
C)  D)
D) 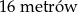
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 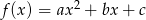 , której miejsca zerowe to:
, której miejsca zerowe to: 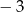 i 2. Do wykresu tego należy punkt
i 2. Do wykresu tego należy punkt 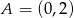 .
.
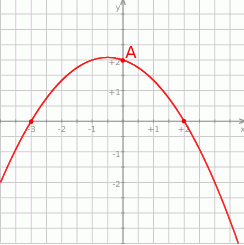
Współczynnik  we wzorze funkcji
we wzorze funkcji 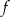 jest równy
jest równy
A) 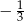 B)
B) 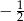 C)
C) 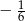 D)
D) 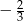
Jeśli funkcja kwadratowa 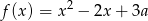 ma dwa miejsca zerowe, to liczba
ma dwa miejsca zerowe, to liczba  spełnia warunek
spełnia warunek
A) 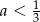 B)
B) 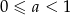 C)
C) 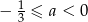 D)
D) 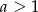
Kąt wpisany w okrąg o średnicy 8, który jest oparty na łuku długości 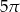 ma miarę
ma miarę
A) 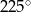 B)
B) 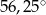 C)
C) 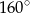 D)
D) 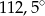
Dane są dwa okręgi styczne zewnętrznie o promieniach 4 i 10. Odległość między środkami tych okręgów jest równa
A) 6 B) 8 C) 14 D) 10
Jeśli 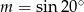 , to
, to
A) 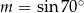 B)
B) 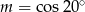 C)
C) 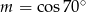 D)
D) 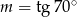
Dany jest ciąg arytmetyczny 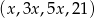 . Wtedy
. Wtedy
A) 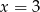 B)
B) 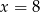 C)
C) 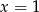 D)
D) 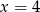
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 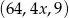 . Stąd wynika, że
. Stąd wynika, że
A) 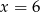 B)
B) 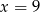 C)
C) 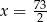 D)
D) 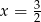
Odcinek 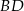 jest zawarty w dwusiecznej kąta ostrego
jest zawarty w dwusiecznej kąta ostrego 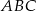 trójkąta prostokątnego, w którym przyprostokątne
trójkąta prostokątnego, w którym przyprostokątne 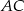 i
i 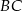 mają długości odpowiednio 8 i 3.
mają długości odpowiednio 8 i 3.
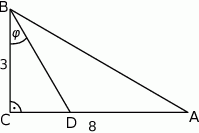
Wówczas miara 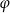 kąta
kąta 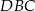 spełnia warunek
spełnia warunek
A) 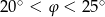 B)
B) 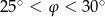 C)
C) 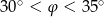 D)
D) 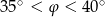
Na rysunku przedstawiona jest prosta 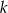 , przechodząca przez punkt
, przechodząca przez punkt 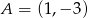 oraz przecinająca oś
oraz przecinająca oś 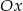 w punkcie
w punkcie 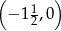 .
.
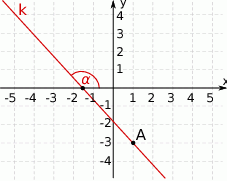
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
A) 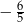 B)
B) 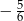 C)
C) 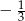 D)
D) 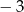
Punkty 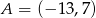 i
i 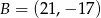 są końcami odcinka
są końcami odcinka 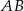 . Obrazem tego odcinka w symetrii względem osi
. Obrazem tego odcinka w symetrii względem osi 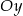 układu współrzędnych jest odcinek
układu współrzędnych jest odcinek 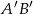 . Środkiem odcinka
. Środkiem odcinka 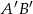 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 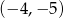 B)
B) 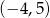 C)
C) 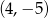 D)
D) 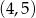
Szklane naczynie w kształcie stożka o promieniu podstawy 8 cm i wysokości 9 cm napełniono wodą do 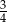 wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
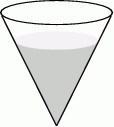
Objętość wody w naczyniu jest równa
A) 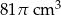 B)
B) 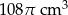 C)
C) 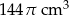 D)
D) 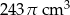
Okrąg opisany na sześciokącie foremnym ma promień 6. Promień okręgu wpisanego w ten sześciokąt jest równy
A) 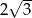 B)
B) 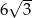 C)
C) 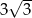 D)
D) 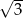
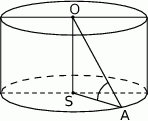
Promień 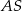 podstawy walca jest równy wysokości
podstawy walca jest równy wysokości 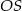 tego walca. Tangens kąta
tego walca. Tangens kąta 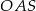 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 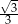 B)
B) 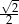 C)
C) 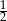 D) 1
D) 1
Średnia arytmetyczna zestawu danych:
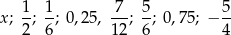
jest równa 0,25. Wtedy mediana tego zestawu danych jest równa
A) 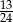 B)
B) 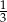 C)
C) 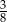 D)
D) 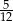
Krawędź podstawy graniastosłupa prawidłowego trójkątnego stanowi  wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
wysokości graniastosłupa. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i jeden wierzchołek drugiej podstawy (patrz rysunek).
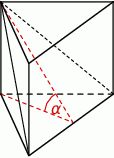
Płaszczyzna przekroju tworzy z podstawą graniastosłupa kąt  o mierze
o mierze
A) 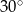 B)
B) 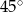 C)
C) 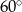 D)
D) 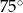
Zadania otwarte
Przeciwprostokątna trójkąta prostokątnego ma długość 34 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Rozwiąż nierówność 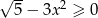 .
.
Dany jest ciąg arytmetyczny 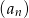 , określony dla
, określony dla 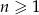 , w którym spełniona jest równość
, w którym spełniona jest równość 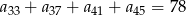 . Oblicz sumę
. Oblicz sumę 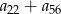 .
.
Ze zbioru liczb 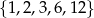 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 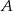 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą parzystą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą parzystą.
Wykaż, że
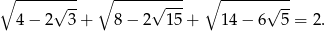
Suma trzech początkowych wyrazów rosnącego ciągu geometrycznego 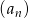 , określonego dla
, określonego dla 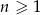 , jest równa
, jest równa 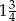 . Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego
. Te same liczby stanowią pierwszy, drugi oraz czwarty wyraz ciągu arytmetycznego 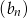 ,
, 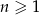 . Wyznacz wzór ciągu
. Wyznacz wzór ciągu 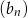 .
.
W trapezie 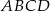 o podstawach
o podstawach 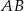 i
i 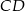 dane są długości przekątnych
dane są długości przekątnych 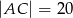 i
i 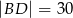 oraz pola
oraz pola 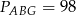 i
i 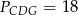 . Punkty
. Punkty 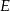 i
i 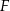 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 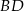 i
i 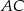 .
.
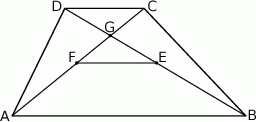
Oblicz pole trójkąta 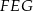 .
.
Punkt 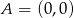 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 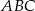 , którego wierzchołek
, którego wierzchołek 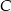 leży na osi
leży na osi 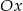 , a wierzchołek
, a wierzchołek 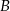 na osi
na osi 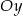 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 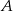 przecina przeciwprostokątną
przecina przeciwprostokątną 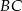 w punkcie
w punkcie 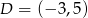 .
.
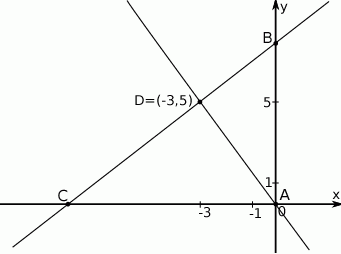
Oblicz współrzędne wierzchołków 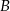 i
i 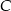 tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej 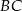 .
.
Podstawą ostrosłupa 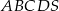 jest romb o boku długości 6. Krawędź boczna
jest romb o boku długości 6. Krawędź boczna 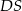 ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).
ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).
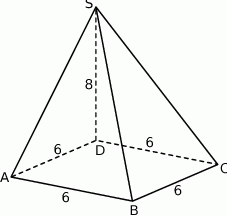
Oblicz objętość tego ostrosłupa.

