/Szkoła średnia
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa I
2 czerwca 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba 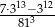 jest równa
jest równa
A) 22 B) 20 C) 7 D) 21
Liczba 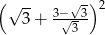 jest równa
jest równa
A) 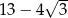 B) 11 C)
B) 11 C) 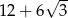 D) 3
D) 3
Wartość wyrażenia 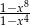 dla
dla 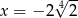 jest równa
jest równa
A) 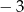 B)
B) 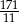 C) 33 D)
C) 33 D) 
Liczba 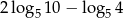 jest równa
jest równa
A) 2 B) 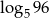 C)
C) 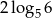 D) 5
D) 5
Dane są liczby 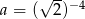 oraz
oraz 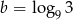 . Zatem
. Zatem
A) 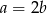 B)
B) 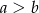 C)
C) 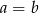 D)
D) 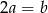
W klasie Ia jest o 25% więcej uczniów niż w klasie Ib. Stąd wynika, że w klasie Ib jest mniej uczniów niż w klasie Ia o
A) 25% B) 75% C) 20% D) 50%
Wyrażenie 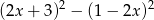 jest równe
jest równe
A) 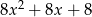 B)
B) 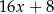 C)
C) 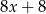 D)
D) 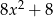
Liczba 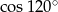 jest równa liczbie
jest równa liczbie
A) 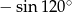 B)
B) 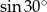 C)
C) 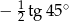 D)
D) 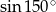
Rozwiązaniem równania 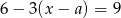 z niewiadomą
z niewiadomą  jest liczba 2. Zatem
jest liczba 2. Zatem
A) 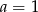 B)
B) 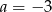 C)
C) 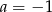 D)
D) 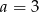
W wycieczce szkolnej wzięło udział 42 uczniów klas pierwszych, 16 uczniów klas drugich i 28 uczniów klas trzecich. Na stronie internetowej szkoły podano informację, że w wyjeździe uczestniczyło w przybliżeniu 90 uczniów. Błąd względny takiego przybliżenia wynosi
A) 4 B) 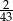 C)
C) 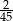 D)
D) 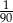
Zbiorem rozwiązań nierówności 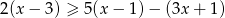 jest
jest
A) zbiór liczb rzeczywistych B) zbiór pusty C) 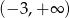 D)
D) 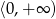
Dany jest zbiór 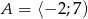 . Liczb pierwszych, które należą do tego zbioru jest
. Liczb pierwszych, które należą do tego zbioru jest
A) 4 B) 5 C) 3 D) 6
Wiadomo, że  jest kątem ostrym oraz
jest kątem ostrym oraz 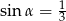 . Wówczas
. Wówczas
A) 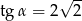 B)
B) 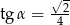 C)
C) 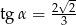 D)
D) 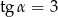
Punkt 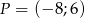 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  (w standardowym położeniu w układzie współrzędnych). Zatem
(w standardowym położeniu w układzie współrzędnych). Zatem 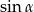 jest równy
jest równy
A) 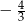 B)
B) 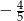 C)
C) 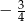 D)
D) 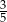
Dany jest trójkąt prostokątny (patrz rysunek).
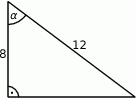
Wartość wyrażenia 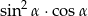 wynosi
wynosi
A) 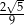 B)
B)  C)
C) 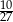 D)
D) 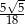
W trójkącie 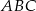 miary kątów wynoszą:
miary kątów wynoszą: 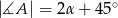 ,
, 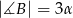 ,
, 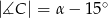 . Wówczas
. Wówczas
A) 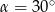 B)
B) 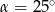 C)
C) 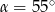 D)
D) 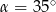
Boki trójkąta 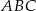 mają długości 12 cm, 15 cm, 18 cm. Trójkąt
mają długości 12 cm, 15 cm, 18 cm. Trójkąt 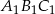 jest podobny do trójkąta
jest podobny do trójkąta 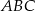 . Najdłuższy bok trójkąta
. Najdłuższy bok trójkąta 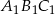 ma długość 6 cm. Obwód trójkąta
ma długość 6 cm. Obwód trójkąta 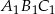 jest równy
jest równy
A) 15 cm B) 45 cm C) 22,5 cm D) 9 cm
Pole trójkąta prostokątnego równoramiennego jest równe 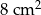 . Przeciwprostokątna tego trójkąta ma długość
. Przeciwprostokątna tego trójkąta ma długość
A) 8 cm B) 4 cm C) 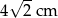 D)
D) 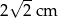
Długość boku trójkąta równobocznego wynosi 8. Pole koła opisanego na tym trójkącie jest równe
A) 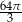 B)
B) 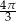 C)
C) 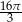 D)
D) 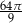
Punkt 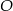 jest środkiem okręgu (rysunek).
jest środkiem okręgu (rysunek).
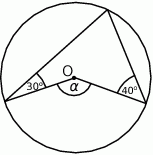
Miara kąta  jest równa
jest równa
A) 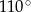 B)
B) 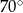 C)
C) 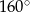 D)
D) 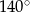
Długości boków trójkąta prostokątnego wynoszą 8 cm, 15 cm, 17 cm. Odcinek łączący środek przeciwprostokątnej z wierzchołkiem kąta prostego tego trójkąta ma długość
A) 8 cm B) 7,5 cm C) 9 cm D) 8,5 cm
Funkcja 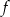 określona jest wzorem
określona jest wzorem 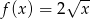 dla
dla 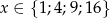 . Do zbioru wartości tej funkcji nie należy liczba
. Do zbioru wartości tej funkcji nie należy liczba
A) 2 B) 5 C) 6 D) 4
Miejscem zerowym funkcji 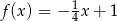 jest liczba
jest liczba
A) 1 B) 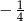 C) 4 D)
C) 4 D) 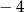
W trójkącie równoramiennym miara kąta przy podstawie jest równa 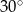 , a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
, a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
A) 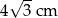 B) 4 cm C)
B) 4 cm C) 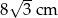 D)
D) 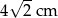
Zadania otwarte
Rozwiąż równanie 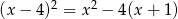 .
.
Reszta z dzielenia liczby  przez 3 jest równa 2. Reszta z dzielenia liczby
przez 3 jest równa 2. Reszta z dzielenia liczby 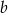 przez 3 jest równa 1. Wykaż, że różnica kwadratów liczb
przez 3 jest równa 1. Wykaż, że różnica kwadratów liczb  i
i 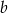 jest podzielna przez 3.
jest podzielna przez 3.
Wiedząc, że 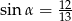 i
i 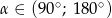 , oblicz
, oblicz 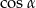 oraz
oraz 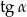 .
.
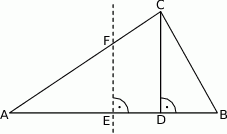
W trójkącie 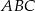 wysokość
wysokość 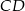 dzieli bok
dzieli bok 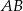 na odcinki
na odcinki 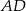 i
i 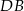 (rysunek), przy czym
(rysunek), przy czym 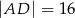 i
i 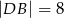 . Wykaż, że symetralna boku
. Wykaż, że symetralna boku 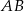 dzieli bok
dzieli bok 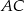 w stosunku 3:1.
w stosunku 3:1.
Przyprostokątna trójkąta prostokątnego ma długość 10. Miara kąta ostrego leżącego naprzeciw tej przyprostokątnej wynosi 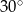 . Oblicz pole koła opisanego na tym trójkącie.
. Oblicz pole koła opisanego na tym trójkącie.
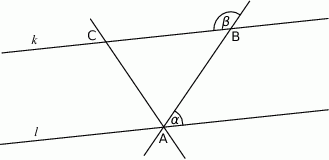
Proste 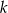 i
i 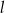 na poniższym rysunku są równoległe oraz
na poniższym rysunku są równoległe oraz 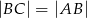 . Kąt
. Kąt 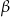 jest o
jest o 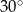 większy od podwojonego kąta
większy od podwojonego kąta  . Oblicz miarę
. Oblicz miarę 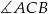 .
.
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w klasie 1a.
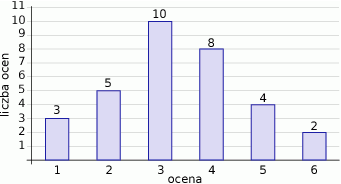
- Jaki procent uczniów tej klasy otrzymał ze sprawdzianu ocenę co najmniej dostateczny?
- O ile procent więcej uczniów otrzymało ocenę dostateczny niż ocenę celujący?
Poniżej przedstawiony jest wykres funkcji 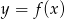 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
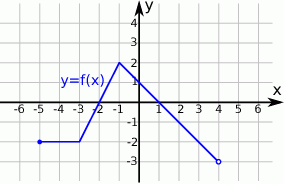
- dziedzinę i zbiór wartości funkcji
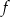 ;
; - maksymalne przedziały, w których funkcja jest malejąca;
- zbiór argumentów, dla których funkcja przyjmuje wartości nieujemne;
- zbiór rozwiązań nierówności
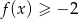 .
.
Dane są liczby
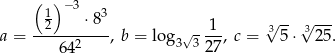
Sprawdź, które z liczb 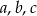 spełniają równanie
spełniają równanie 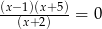 .
.
Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy 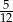 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.

