/Szkoła średnia
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 2 czerwca 2023 Czas pracy: 180 minut
Dane są liczby
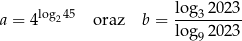
Oblicz 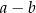 .
.
Wśród  osób są Ania i jej dwaj znajomi. Wszystkie te
osób są Ania i jej dwaj znajomi. Wszystkie te  osób ustawiamy w kolejkę jedna za drugą. Liczba wszystkich takich ustawień jest 12 razy większa od liczby wszystkich takich ustawień tych
osób ustawiamy w kolejkę jedna za drugą. Liczba wszystkich takich ustawień jest 12 razy większa od liczby wszystkich takich ustawień tych  osób w kolejkę, w których Ania i jej dwaj znajomi zajmują trzy kolejne miejsca (w dowolnej kolejności). Oblicz
osób w kolejkę, w których Ania i jej dwaj znajomi zajmują trzy kolejne miejsca (w dowolnej kolejności). Oblicz  .
.
Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe 0,1. Oblicz prawdopodobieństwo zdarzenia 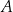 polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Funkcja 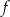 jest określona wzorem
jest określona wzorem 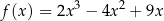 dla każdego
dla każdego 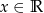 . Punkt
. Punkt 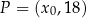 należy do wykresu funkcji
należy do wykresu funkcji 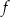 . Oblicz
. Oblicz 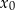 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 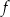 w punkcie
w punkcie 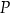 .
.
Wykaż, że dla każdej liczby rzeczywistej dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność
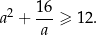
Dany jest okrąg 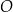 . Przez punkt
. Przez punkt 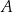 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 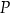 oraz
oraz 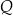 . Przez punkt
. Przez punkt 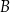 leżący na odcinku
leżący na odcinku 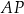 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 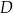 , która przecięła odcinek
, która przecięła odcinek 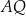 w punkcie
w punkcie 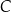 (zobacz rysunek).
(zobacz rysunek).
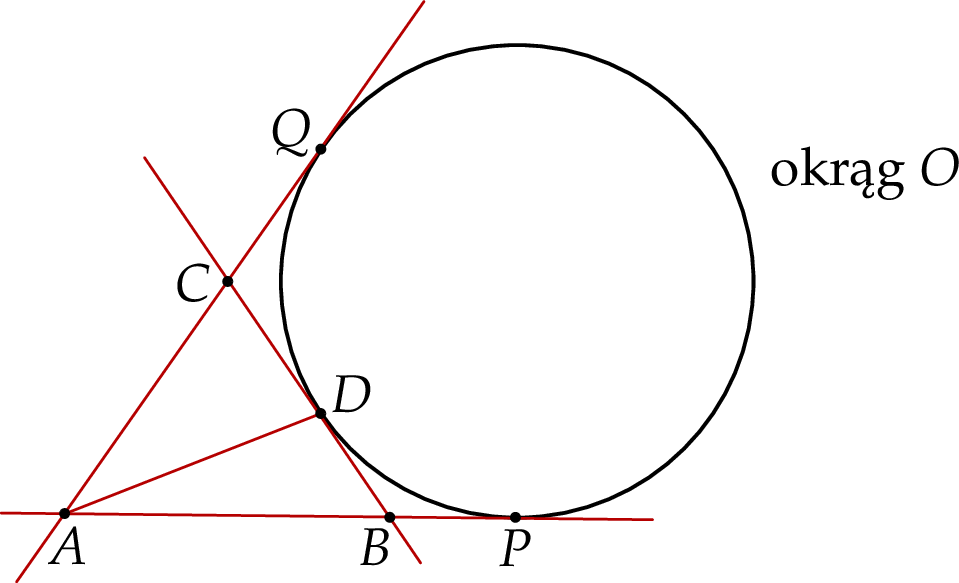
Wykaż, że jeżeli 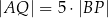 oraz
oraz 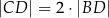 , to trójkąt
, to trójkąt 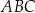 jest równoramienny.
jest równoramienny.
Dany jest nieskończony szereg geometryczny
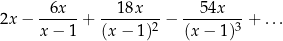
Wyznacz wszystkie wartości zmiennej  (różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest równa
(różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest równa 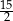 .
.
Rozwiąż równanie 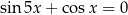 w zbiorze
w zbiorze ![[− π-, π] 2 2](https://img.zadania.info/zes/0081303/HzesT34x.png) .
.
W okrąg o równaniu 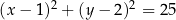 wpisano trójkąt
wpisano trójkąt 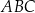 . Bok
. Bok 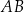 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 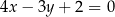 . Wysokość
. Wysokość 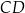 tego trójkąta dzieli bok
tego trójkąta dzieli bok 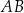 tak, że
tak, że 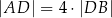 . Oblicz pole trójkąta
. Oblicz pole trójkąta 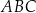 .
.
Wyznacz wszystkie wartości parametru 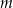 , dla których równanie
, dla których równanie
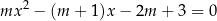
ma dokładnie dwa różne rozwiązania rzeczywiste 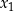 oraz
oraz 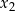 , spełniające warunki:
, spełniające warunki:
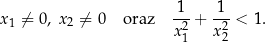
Ciąg 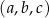 jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
jest trzywyrazowym ciągiem geometrycznym o wyrazach dodatnich. Ciąg
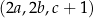
jest trzywyrazowym ciągiem arytmetycznym. Ponadto, spełniony jest warunek 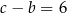 . Oblicz
. Oblicz 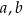 oraz
oraz  .
.
Czworokąt wypukły 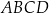 jest wpisany w okrąg o promieniu 4. Kąty
jest wpisany w okrąg o promieniu 4. Kąty 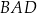 i
i 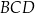 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 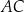 i
i 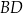 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 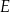 tak, że
tak, że 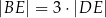 oraz
oraz 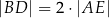 .
.

Oblicz długości boków czworokąta 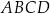 .
.
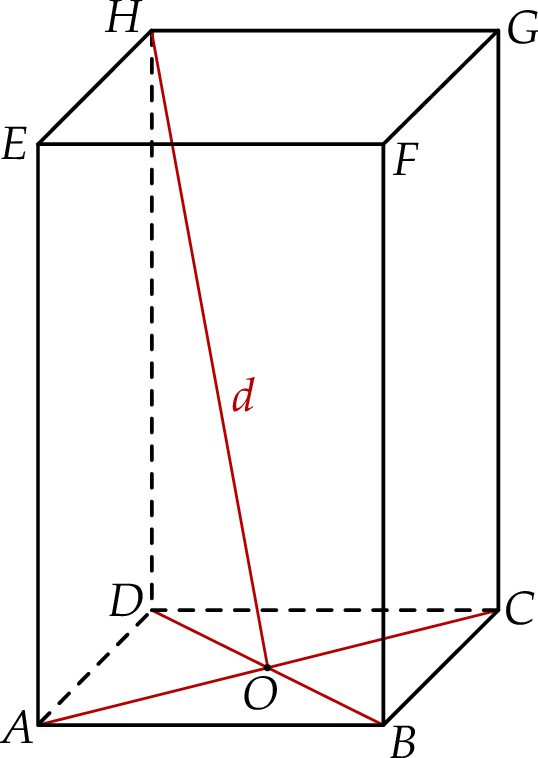
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne 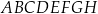 , w których odcinek łączący punkt
, w których odcinek łączący punkt 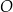 przecięcia przekątnych
przecięcia przekątnych 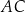 i
i 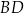 podstawy
podstawy 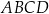 z dowolnym wierzchołkiem podstawy
z dowolnym wierzchołkiem podstawy 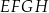 ma długość
ma długość 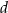 (zobacz rysunek).
(zobacz rysunek).
-
Wyznacz zależność objętości
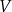 graniastosłupa od jego wysokości
graniastosłupa od jego wysokości 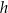 i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 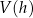 .
. -
Wyznacz wysokość tego z rozważanych graniastosłupów, którego objętość jest największa.

