/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 20 marca 2021 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 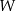 określony wzorem
określony wzorem 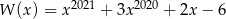
A) jest podzielny przez 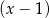 i z dzielenia przez
i z dzielenia przez 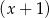 daje resztę równą
daje resztę równą 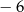 .
.
B) jest podzielny przez 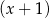 i z dzielenia przez
i z dzielenia przez 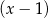 daje resztę równą
daje resztę równą 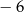 .
.
C) jest podzielny przez 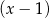 i jest podzielny przez
i jest podzielny przez 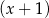 .
.
D) nie jest podzielny ani przez 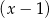 , ani przez
, ani przez 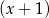 .
.
Liczba 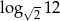 jest równa
jest równa
A) 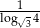 B)
B) 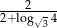 C)
C) 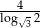 D)
D) 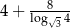
Proste 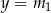 i
i 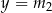 , gdzie
, gdzie 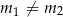 są styczne do wykresu funkcji
są styczne do wykresu funkcji 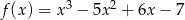 w punktach
w punktach 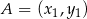 i
i 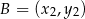 . Zatem
. Zatem
A) 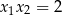 B)
B) 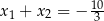 C)
C) 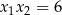 D)
D) 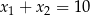
Liczba  jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie 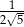 . Liczba
. Liczba 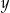 jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie 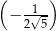 . Wynika stąd, że liczba
. Wynika stąd, że liczba 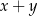 jest równa
jest równa
A) 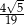 B)
B) 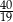 C)
C) 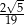 D)
D) 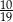
Zadania otwarte
W trójkącie 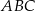 długość boku
długość boku 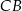 stanowi
stanowi 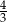 długości boku
długości boku 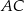 , a kąt
, a kąt 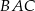 ma miarę
ma miarę 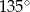 . Oblicz cosinus kąta
. Oblicz cosinus kąta 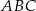 .
.
O zdarzeniach 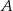 i
i 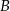 wiadomo, że
wiadomo, że 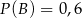 ;
; 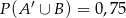 ;
; 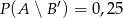 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 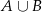 .
.
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 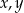 prawdziwa jest nierówność
prawdziwa jest nierówność
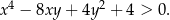
Cztery liczby tworzą ciąg geometryczny, przy czym suma pierwszej i czwartej jest równa 52, a iloczyn drugiej i trzeciej jest równy 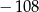 . Wyznacz te liczby.
. Wyznacz te liczby.
Rozwiąż równanie 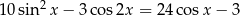 dla
dla 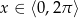 .
.
Reszty z dzielenia wielomianu 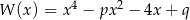 przez dwumiany
przez dwumiany 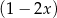 i
i 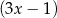 są odpowiednio równe
są odpowiednio równe 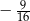 i
i 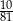 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 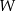 przez dwumian
przez dwumian 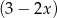 .
.
Oblicz, ile jest dwunastocyfrowych liczb naturalnych, których suma cyfr jest równa 8 i jednocześnie w ich zapisie nie występują cyfry 1 i 4.
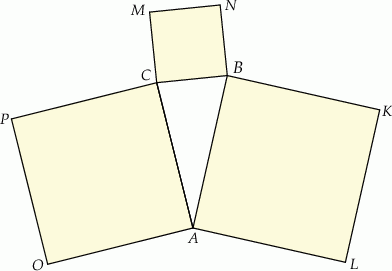
Na bokach trójkąta 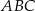 zbudowano kwadraty
zbudowano kwadraty 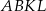 ,
, 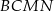 i
i 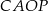 (zobacz rysunek).
(zobacz rysunek).
Kąty 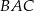 i
i 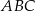 są ostre oraz suma ich tangensów jest równa
są ostre oraz suma ich tangensów jest równa  . Wykaż, że jeżeli pole kwadratu
. Wykaż, że jeżeli pole kwadratu 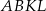 jest pięć razy większe od pola trójkąta
jest pięć razy większe od pola trójkąta 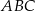 , to suma pól kwadratów
, to suma pól kwadratów 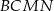 i
i 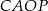 też jest pięć razy większa od pola trójkąta
też jest pięć razy większa od pola trójkąta 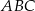 .
.
Podstawą ostrosłupa 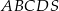 jest trapez
jest trapez 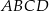 . Przekątna
. Przekątna 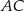 tego trapezu ma długość
tego trapezu ma długość 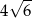 , jest prostopadła do ramienia
, jest prostopadła do ramienia 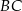 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 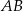 tego trapezu kąt o mierze
tego trapezu kąt o mierze 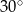 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 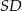 .
.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 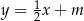 ,
, 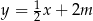 ,
, 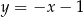 ,
, 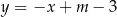 , gdzie
, gdzie 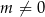 i
i 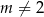 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 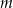 , dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy
, dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy 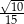 .
.
Firma logistyczna planuje produkcję pojemników w kształcie graniastosłupa prostego o objętości 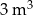 i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za
i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za 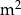 , a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za
, a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za 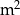 . Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.
. Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.

