Zadanie nr 8218627
Oblicz, ile jest liczb naturalnych czterocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 36.
Rozwiązanie
Sprawdźmy najpierw w jaki sposób możemy 36 napisać jako iloczyn czterech cyfr.
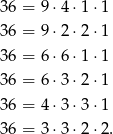
Zajmijmy się najpierw pierwszą sytuacją. Miejsce dla 9-ki możemy wybrać na 4 sposoby, potem na 3 sposoby wybieramy miejsce dla 4-ki i na pozostałych 2 miejscach umieszczamy 1-ki. W sumie jest więc
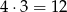
liczb tej postaci. Zauważmy ponadto, że dokładnie taki sam rachunek mamy w przypadku rozkładów
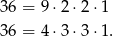
(wybieramy miejsca dla 9-ki i 1-ki, a potem uzupełniamy 2-kami, podobnie dla drugiego rozkładu).
W przypadku trzeciego rozkładu, musimy wybrać miejsca dla 6-ek, a na pozostałych miejscach wpisujemy 1-ki. Możemy to zrobić na
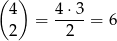
sposobów. Jest więc 6 takich liczb. Dokładnie tyle samo jest liczb z ostatnim rozkładem (na 6 sposobów wybieramy miejsca dla 3-ek).
Pozostał 4 rozkład – w tym rozkładzie żadne cyfry się nie powtarzają, więc są
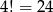
możliwości ustawienia cyfr.
W sumie jest więc
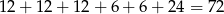
liczb spełniających warunki zadania.
Odpowiedź: 72

