/Szkoła średnia
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom rozszerzony grupa II 2 czerwca 2015 Czas pracy: 180 minut
Zadania zamknięte
Zbiorem rozwiązań nierówności 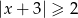 jest:
jest:
A) 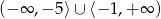 B)
B) 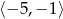 C)
C) 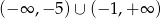 D)
D) 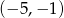
Liczba 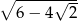 jest równa
jest równa
A) 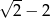 B)
B) 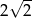 C)
C) 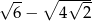 D)
D) 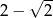
Wartość wyrażenia 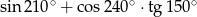 jest równa
jest równa
A) 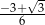 B)
B) 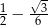 C)
C) 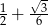 D)
D) 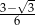
Dany jest trójkąt równoramienny 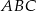 . Kąt
. Kąt 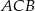 ma miarę
ma miarę 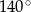 , a dwusieczna kąta
, a dwusieczna kąta 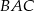 przecina bok
przecina bok 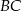 w punkcie
w punkcie 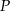 . Miara kąta
. Miara kąta 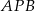 jest równa
jest równa
A) 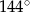 B)
B) 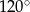 C)
C) 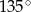 D)
D) 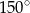
Błąd względny przybliżenia liczby 0,08 liczbą 0,1 jest równy
A) 1,25% B) 12,5% C) 25% D) 2,5%
Zadania otwarte
Cenę książki obniżono o 10%, a następnie podwyższono o 20%. Obecna cena książki stanowi 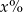 ceny początkowej. Oblicz
ceny początkowej. Oblicz  .
.
Zapisz liczbę 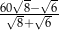 w postaci
w postaci 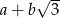 , gdzie
, gdzie  i
i 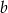 są liczbami całkowitymi.
są liczbami całkowitymi.
Suma kątów wpisanego i środkowego opartych na tym samym łuku wynosi 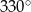 . Oblicz miarę kąta wpisanego.
. Oblicz miarę kąta wpisanego.
Oblicz wartość wyrażenia 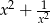 , gdy
, gdy 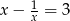 .
.
Rozwiąż równanie 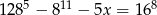 .
.
Niech 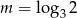 . Wykaż, że
. Wykaż, że 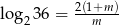 .
.
Skróć wyrażenie 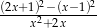 . Podaj konieczne założenia.
. Podaj konieczne założenia.
W trójkącie 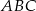 bok
bok 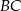 ma długość 12 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku
ma długość 12 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku 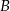 jest równa
jest równa 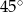 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 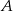 jest równa
jest równa 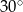 .
.
W trójkącie 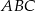 symetralna boku
symetralna boku 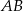 dzieli bok
dzieli bok 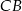 na odcinki długości
na odcinki długości 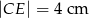 i
i 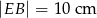 . Bok
. Bok 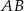 ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość
ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość 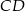 podzieliła bok
podzieliła bok 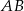 .
.
W trójkącie równobocznym wysokość jest o 3 cm krótsza od boku trójkąta. Oblicz pole i obwód tego trójkąta.
Reszta z dzielenia liczby całkowitej  przez 5 jest równa 4. Wyznacz resztę z dzielenia liczby
przez 5 jest równa 4. Wyznacz resztę z dzielenia liczby 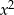 przez 5.
przez 5.
Rozwiąż równanie 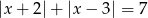 .
.
Udowodnij, że w trójkącie równoramiennym środkowe poprowadzone do równych boków są równej długości.

