/Szkoła średnia

Zadanie nr 8543862

Dodaj do ulubionych
Dodaj do rozwiązanych

Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 60 km. Jadąc z domu nad jezioro poruszał się z prędkością o 2 km/h większą niż w drodze powrotnej i pokonał trasę w czasie o 10 minut krótszym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?

Rozwiązanie

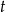Jeżeli przez v oznaczymy średnią prędkość rowerzysty a przez t czas w którym przejechał 30 km (czyli drogę do jeziora), to wiemy, że

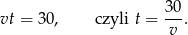
vt = 30 , czyli t = 30. v

Wiemy ponadto, że w drodze powrotnej średnia prędkość była mniejsza o 2 km/h oraz czas przejazdu był dłuższy o 10 minut. Otrzymujemy stąd równanie:

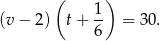
( ) 1- (v− 2) t+ 6 = 30.

Po podstawieniu za 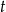t z poprzedniej równości dostajemy:

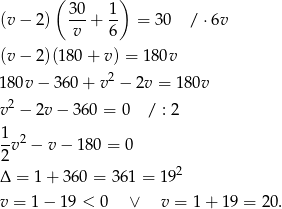
( ) 30- 1- (v− 2) v + 6 = 30 / ⋅ 6v (v− 2)(180 + v) = 18 0v 180v − 360 + v2 − 2v = 180v v2 − 2v− 360 = 0 / : 2 1 -v2 − v − 180 = 0 2 Δ = 1 + 36 0 = 361 = 192 v = 1 − 19 < 0 ∨ v = 1 + 19 = 2 0.

Oczywiście pierwsze rozwiązanie odrzucamy i mamy 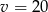v = 2 0 . W takim razie w drodze powrotnej rowerzysta poruszał się z prędkością 18 km/h i pokonał tę drogę w czasie

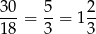
3-0 5- 2- 1 8 = 3 = 13

godziny.  
Odpowiedź: 18 km/h, 1 godzina i 40 minut

Wersja PDF