/Szkoła średnia

Zadanie nr 8609778

Dodaj do ulubionych
Dodaj do rozwiązanych

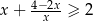Wykaż, że dla dowolnej liczby dodatniej x prawdziwa jest nierówność x + 4−x2x≥ 2 .

Rozwiązanie

Sposób I

Przekształcamy daną nierówność w sposób równoważny. Ponieważ 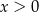x > 0 , możemy nierówność pomnożyć stronami przez x .

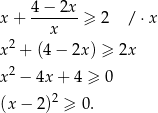
x + 4-−-2x- ≥ 2 /⋅ x x x2 + (4 − 2x) ≥ 2x x2 − 4x + 4 ≥ 0 2 (x − 2) ≥ 0.

Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być prawdziwa.

Sposób II

Przekształcamy nierówność w sposób równoważny.

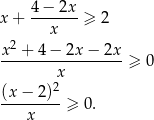
4−--2x- x + x ≥ 2 2 x-+--4−--2x−--2x-≥ 0 x (x− 2)2 ---------≥ 0. x

Otrzymana nierówność jest oczywiście spełniona (bo 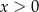x > 0 ), więc wyjściowa nierówność też musi być prawdziwa.

Wersja PDF