/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 25 kwietnia 2015 Czas pracy: 170 minut
Zadania zamknięte
Pierwiastek równania 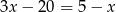 zaokrąglono do wartości 6,2. Błąd względny tego przybliżenia to
zaokrąglono do wartości 6,2. Błąd względny tego przybliżenia to
A) 8% B) 0,8% C) 0,08% D) 0,97%
Kwadrat 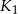 o wierzchołkach
o wierzchołkach 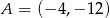 ,
, 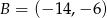 ,
, 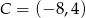 i
i 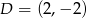 przekształcono w symetrii względem osi
przekształcono w symetrii względem osi 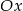 i otrzymano kwadrat
i otrzymano kwadrat 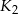 . Odległość między środkami kwadratów
. Odległość między środkami kwadratów 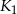 i
i 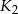 jest równa
jest równa
A) 4 B) 8 C) 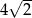 D)
D) 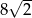
Wojtek 40% swoich oszczędności przeznaczył na zakup nowego plecaka. Połowę z tego, co mu zostało, przeznaczył na zakup butów. Ile procent oszczędności pozostało Wojtkowi?
A) 10% B) 30% C) 40% D) 20%
Liczba 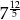 jest równa
jest równa
A) 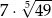 B)
B) 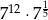 C)
C) 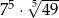 D)
D) 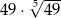
Pierwiastki 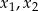 równania
równania 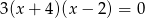 spełniają warunek
spełniają warunek
A) 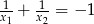 B)
B) 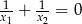 C)
C) 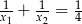 D)
D) 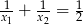
Wyrażenie 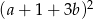 jest równe
jest równe
A) 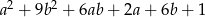
B) 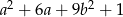
C) 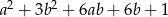
D) 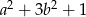
Liczba 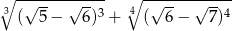 jest równa
jest równa
A) 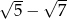 B)
B) 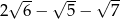 C)
C) 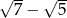 D)
D) 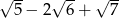
Nierówność 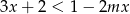 jest sprzeczna jeżeli
jest sprzeczna jeżeli
A) 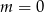 B)
B) 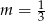 C)
C) 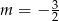 D)
D) 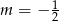
O funkcji liniowej 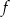 wiadomo, że
wiadomo, że 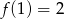 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 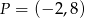 . Wzór funkcji
. Wzór funkcji 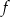 to
to
A) 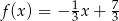 B)
B) 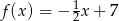 C)
C) 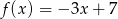 D)
D) 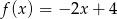
Reszta z dzielenia liczby 65 przez 7 jest równa
A) 1 B) 2 C) 3 D) 5
Funkcja 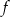 , określona dla wszystkich liczb naturalnych, przyporządkowuje liczbie
, określona dla wszystkich liczb naturalnych, przyporządkowuje liczbie  ostatnią cyfrę liczby
ostatnią cyfrę liczby 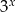 . Zbiór wartości funkcji
. Zbiór wartości funkcji 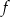 zawiera dokładnie
zawiera dokładnie
A) 2 elementy. B) 4 elementy. C) 6 elementów. D) 9 elementów.
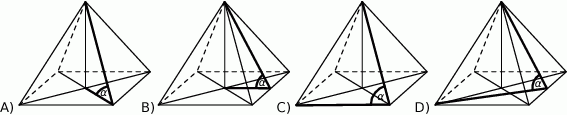
Kąt  nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
Obwód równoległoboku 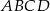 o wierzchołkach
o wierzchołkach 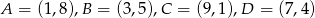 jest równy
jest równy
A) 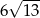 B)
B) 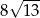 C)
C) 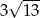 D)
D) 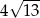
Na rysunku przedstawiono wykres funkcji kwadratowej postaci 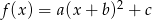 .
.
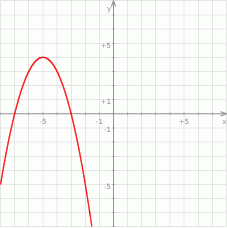
Zatem
A) 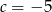 B)
B) 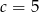 C)
C) 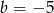 D)
D) 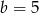
Rozwiązaniem równania 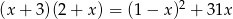 jest:
jest:
A) 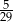 B)
B) 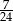 C)
C) 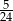 D)
D) 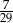
Liczba 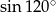 jest równa liczbie
jest równa liczbie
A) 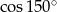 B)
B) 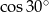 C)
C) 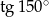 D)
D) 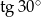
Pole trójkąta 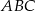 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
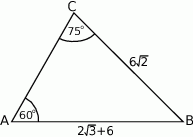
A) 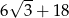 B)
B) 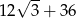 C)
C) 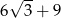 D)
D) 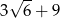
Przekrój osiowy stożka jest trójkątem równobocznym o wysokości 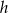 . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 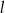 oznacza długość jego tworzącej, to
oznacza długość jego tworzącej, to
A) 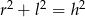 B)
B) 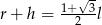 C)
C) 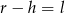 D)
D) 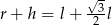
Mediana danych 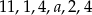 jest równa 3. Wówczas
jest równa 3. Wówczas
A) 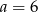 B)
B) 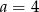 C)
C) 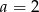 D)
D) 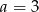
Wskaż liczbę, która spełnia równanie 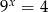 .
.
A) 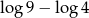 B)
B) 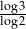 C)
C) 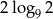 D)
D) 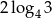
Dany jest nieskończony rosnący ciąg geometryczny 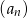 o wyrazach dodatnich, gdzie
o wyrazach dodatnich, gdzie 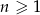 . Wtedy
. Wtedy
A) 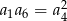 B)
B) 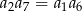 C)
C) 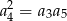 D)
D) 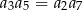
Wyraz ogólny ciągu 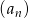 ma postać
ma postać 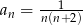 , gdzie
, gdzie 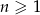 . Wobec tego
. Wobec tego
A) 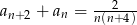
B) 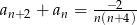
C) 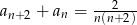
D) 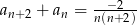
Z każdego ze zbiorów 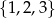 i
i 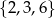 wybieramy po jednej liczbie i obliczamy ich iloczyn. Niech
wybieramy po jednej liczbie i obliczamy ich iloczyn. Niech 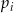 będzie prawdopodobieństwem otrzymania
będzie prawdopodobieństwem otrzymania 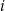 w wyniku tego działania. Wtedy
w wyniku tego działania. Wtedy
A) 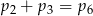 B)
B) 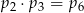 C)
C) 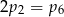 D)
D) 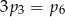
Zadania otwarte
Rozwiąż równanie 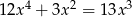 .
.
Wykresem funkcji kwadratowej 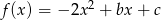 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 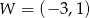 . Oblicz wartości współczynników
. Oblicz wartości współczynników 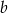 i
i  .
.
Uzasadnij, że liczba 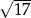 spełnia nierówność
spełnia nierówność 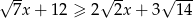 .
.
Niech 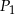 będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty
będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty 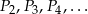 w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
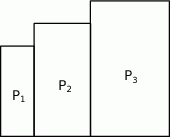
Wyznacz liczbę  , dla której obwód prostokąta
, dla której obwód prostokąta 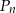 jest równy 246.
jest równy 246.
Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po  okresach rozpadu połowicznego wyraża się wzorem
okresach rozpadu połowicznego wyraża się wzorem 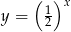 .
.
W przypadku izotopu radu 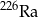 czas połowicznego rozpadu jest równy 1600 lat. Po ilu latach z 1 g
czas połowicznego rozpadu jest równy 1600 lat. Po ilu latach z 1 g 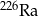 pozostanie nie więcej niż 6,25% masy tego pierwiastka?
pozostanie nie więcej niż 6,25% masy tego pierwiastka?
Uzasadnij, że jeżeli liczba całkowita jest nieparzysta, to jej kwadrat przy dzieleniu przez 8 daje resztę 1.
Na trójkącie o bokach długości 15, 20, 25 opisano okrąg. Oblicz długość środkowej tego trójkąta poprowadzonej do środka najdłuższego boku.
Wybieramy losowo 2 kostki z tabliczki czekolady przedstawionej na poniższym rysunku.

Oblicz prawdopodobieństwo tego, że wybrane dwie kostki są sąsiednie (tzn. mają wspólną krawędź).
Boki 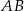 i
i 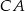 trójkąta
trójkąta 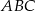 są zawarte w prostych
są zawarte w prostych 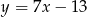 i
i 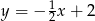 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 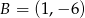 i
i 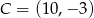 . Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok
. Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok 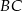 .
.
Kacper i Hela otrzymali identyczne zestawy 138 drewnianych klocków, w których każdy klocek jest sześcianem o krawędzi 2 cm. Kacper ze swoich klocków zbudował graniastosłup prawidłowy czworokątny i zostały mu dwa klocki, których nie było gdzie dołożyć. Hela ze swoich klocków zbudowała trzy identyczne graniastosłupy prawidłowe czworokątne i zostały jej trzy klocki, których nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej graniastosłupa zbudowanego przez Kacpra do pola powierzchni całkowitej jednego z graniastosłupów zbudowanych przez Helę. Wynik podaj w postaci ułamka nieskracalnego.

