/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 5 maja 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba 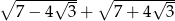 jest równa
jest równa
A) 16 B) 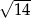 C) 4 D)
C) 4 D) 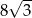
Wyrażenie 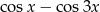 jest równe
jest równe
A) 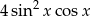 B)
B) 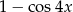 C)
C) 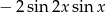 D)
D) 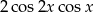
Pierwszy wyraz nieskończonego ciągu geometrycznego jest równy 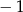 , a suma wszystkich jego wyrazów jest równa ilorazowi tego ciągu. Drugi wyraz tego ciągu jest równy
, a suma wszystkich jego wyrazów jest równa ilorazowi tego ciągu. Drugi wyraz tego ciągu jest równy
A) 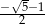 B)
B) 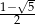 C)
C) 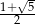 D)
D) 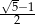
Granica jednostronna 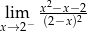
A) nie istnieje B) jest równa 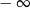 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 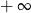
Układ równań 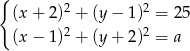 z niewiadomymi
z niewiadomymi 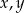 i parametrem dodatnim
i parametrem dodatnim  ma dwa rozwiązania, gdy
ma dwa rozwiązania, gdy
A) 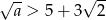 B)
B) 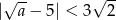 C)
C) 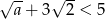 D)
D) 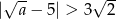
Zadania otwarte
Wyznacz wszystkie wartości parametru 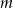 , dla których wśród rozwiązań równania
, dla których wśród rozwiązań równania
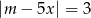
są zarówno liczby dodatnie, jak i ujemne.
Wykaż, że 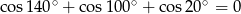 .
.
Na bokach 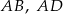 i
i 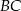 rombu
rombu 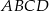 wybrano odpowiednio punkty
wybrano odpowiednio punkty 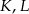 i
i 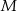 w ten sposób, że odcinki
w ten sposób, że odcinki 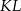 i
i 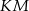 są równoległe do przekątnych rombu. Wykaż, że odcinek
są równoległe do przekątnych rombu. Wykaż, że odcinek 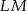 przechodzi przez punkt przecięcia przekątnych rombu.
przechodzi przez punkt przecięcia przekątnych rombu.
Wyznacz maksymalne przedziały monotoniczności funkcji 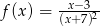 .
.
Rzucamy sześcienną kostką do gry tak długo, aż otrzymamy co najmniej dwie nieparzyste liczby oczek, albo 10 parzystych liczb oczek. Oblicz prawdopodobieństwo, że w przeprowadzonym doświadczeniu otrzymaliśmy liczbę oczek równą 5, przy założeniu, że otrzymaliśmy tylko jedną nieparzystą liczbę oczek.
Ostrosłup prawidłowy trójkątny przecięto płaszczyzną, która przechodzi przez krawędź podstawy długości  oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem
oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Rozwiąż równanie 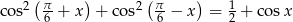 .
.
Wyznacz wszystkie wartości parametru 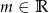 , dla których równanie
, dla których równanie 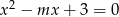 ma dwa różne pierwiastki
ma dwa różne pierwiastki 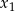 i
i 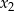 takie, że
takie, że 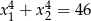 .
.
Wyznacz trzywyrazowy ciąg geometryczny, w którym suma trzech kolejnych wyrazów jest równa 84, a ich iloczyn jest równy 13824.
Z punktu 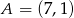 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 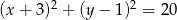 . Oblicz pole trójkąta
. Oblicz pole trójkąta 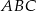 , gdzie
, gdzie 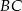 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
W kulę o promieniu długości 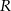 wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.

