/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 23 marca 2024 Czas pracy: 180 minut
Rozwiąż nierówność 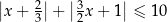 .
.
Oblicz granicę funkcji 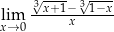 .
.
Pięciokąt 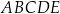 jest wpisany w okrąg. Przekątne
jest wpisany w okrąg. Przekątne 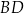 i
i 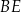 tego pięciokąta przecinają przekątną
tego pięciokąta przecinają przekątną 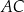 w punktach
w punktach 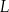 i
i 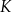 odpowiednio (zobacz rysunek).
odpowiednio (zobacz rysunek).

Udowodnij, że jeżeli punkty 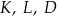 i
i 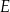 leżą na jednym okręgu, to
leżą na jednym okręgu, to 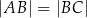 .
.
Liczby rzeczywiste  oraz
oraz 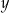 spełniają jednocześnie równanie
spełniają jednocześnie równanie 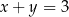 i nierówność
i nierówność
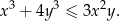
Wykaż, że 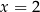 oraz
oraz 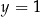 .
.
Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe 0,4. Oblicz prawdopodobieństwo zdarzenia 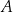 polegającego na tym, że w okresie dziesięciu dni wystąpi 6, 7 lub 8 awarii tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie dziesięciu dni wystąpi 6, 7 lub 8 awarii tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
W trójkącie 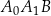 kąt
kąt 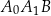 jest prosty,
jest prosty, 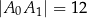 i
i 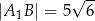 . Odcinek
. Odcinek 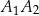 jest wysokością tego trójkąta, odcinek
jest wysokością tego trójkąta, odcinek 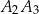 jest wysokością trójkąta
jest wysokością trójkąta 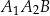 , odcinek
, odcinek 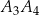 jest wysokością trójkąta
jest wysokością trójkąta 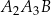 itd. Ogólnie, dla każdej liczby naturalnej
itd. Ogólnie, dla każdej liczby naturalnej 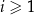 , odcinek
, odcinek 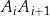 jest wysokością trójkąta
jest wysokością trójkąta 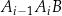
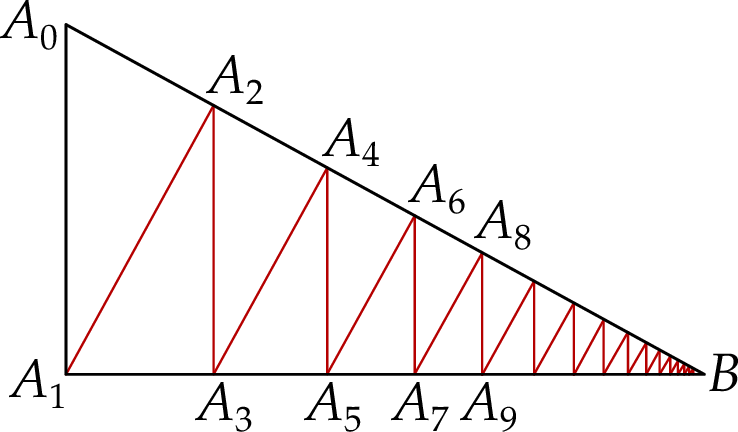
Oblicz długość nieskończonej łamanej 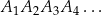 .
.
Wyznacz wszystkie styczne do wykresu funkcji 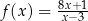 , które razem z osiami układu współrzędnych ograniczają trójkąt równoramienny.
, które razem z osiami układu współrzędnych ograniczają trójkąt równoramienny.
Czworokąt 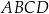 , w którym
, w którym 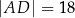 i
i 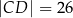 , jest opisany na okręgu. Kąt
, jest opisany na okręgu. Kąt 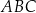 tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie
tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie 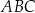 jest równy 12,5. Obwód czworokąta
jest równy 12,5. Obwód czworokąta 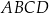 jest równy 66. Oblicz długość przekątnej
jest równy 66. Oblicz długość przekątnej 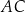 tego czworokąta.
tego czworokąta.
Oblicz sumę wszystkich rozwiązań równania
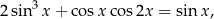
które należą do przedziału ![[− 8π ,24π]](https://img.zadania.info/zes/0086375/HzesT42x.png) .
.
W okrąg o równaniu 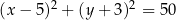 wpisano trójkąt ostrokątny
wpisano trójkąt ostrokątny 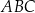 . Bok
. Bok 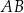 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 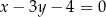 . Wysokość
. Wysokość 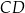 tego trójkąta dzieli bok
tego trójkąta dzieli bok 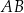 tak, że
tak, że 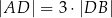 . Oblicz pole trójkąta
. Oblicz pole trójkąta 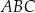 .
.
Wyznacz wszystkie wartości 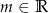 , dla których równanie
, dla których równanie 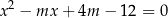 ma dwa różne pierwiastki spełniające nierówność
ma dwa różne pierwiastki spełniające nierówność
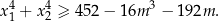
Funkcja 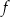 jest określona wzorem
jest określona wzorem
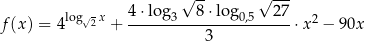
dla każdej liczby dodatniej  .
.
-
Wykaż, że dla każdej liczby dodatniej
 wzór funkcji
wzór funkcji 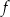 można równoważnie przekształcić do postaci
można równoważnie przekształcić do postaci 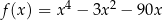 .
. -
Oblicz najmniejszą wartość funkcji
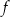 określonej dla każdej liczby dodatniej
określonej dla każdej liczby dodatniej  .
.
Punkty 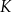 i
i 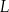 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 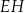 i
i 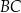 prostopadłościanu
prostopadłościanu 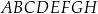 . Przez krawędź
. Przez krawędź 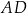 poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy po kątem
poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy po kątem 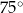 i płaszczyzna ta przecięła odcinek
i płaszczyzna ta przecięła odcinek 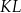 w punkcie
w punkcie 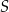 (zobacz rysunek).
(zobacz rysunek).
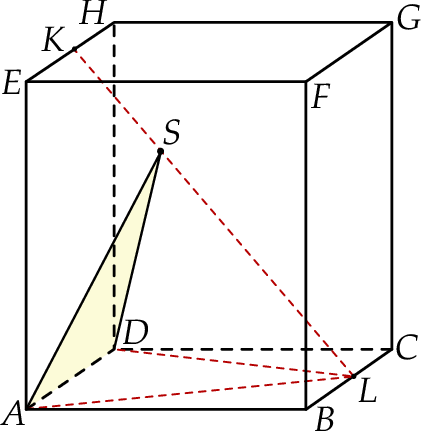
Oblicz pole trójkąta 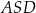 jeżeli
jeżeli 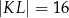 ,
, 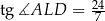 i
i 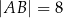 .
.

