/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 4 marca 2017 Czas pracy: 180 minut
Zadania zamknięte
Ile jest liczb  należących do przedziału
należących do przedziału 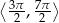 , które spełniają równanie
, które spełniają równanie 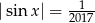 ?
?
A) 2 B) 8 C) 6 D) 4
W rozwinięciu wyrażenia 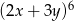 współczynnik przy iloczynie
współczynnik przy iloczynie 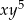 jest równy
jest równy
A) 1458 B) 2916 C) 972 D) 486
Na rysunku przedstawiono fragment wykresu pochodnej 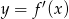 funkcji
funkcji 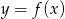 .
.
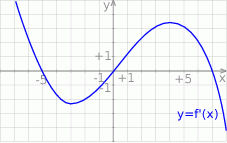
Wynika stąd, że funkcja 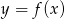 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 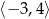 B)
B) 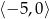 C)
C) 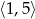 D)
D) 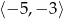
Ile jest liczb naturalnych pięciocyfrowych, w których iloczyn cyfr jest równy 0?
A) 59049 B) 30951 C) 3439 D) 6561
Granica 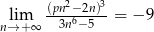 . Wynika stąd, że
. Wynika stąd, że
A) 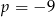 B)
B) 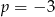 C)
C) 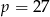 D)
D) 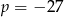
Zadania otwarte
Rozwiąż nierówność 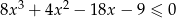 .
.
Dany jest ciąg 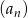 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 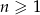 , w którym
, w którym 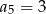 oraz dla każdej liczby
oraz dla każdej liczby 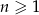 prawdziwa jest równość
prawdziwa jest równość 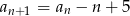 . Oblicz pierwszy wyraz ciągu
. Oblicz pierwszy wyraz ciągu 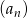 i ustal, czy ciąg ten jest rosnący.
i ustal, czy ciąg ten jest rosnący.
Oblicz wartość wyrażenia 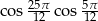 .
.
W trójkącie równoramiennym 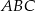 o podstawie
o podstawie 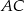 dane są:
dane są: 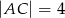 oraz
oraz 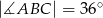 . Odcinek
. Odcinek 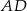 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 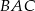 (zobacz rysunek).
(zobacz rysunek).
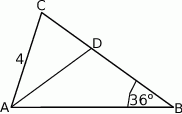
Oblicz długość odcinka 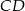 .
.
W urnie znajdują się drewniane klocki, przy czym każdy z klocków jest biały lub czarny oraz każdy z klocków ma kształt kuli lub sześcianu. Wiadomo, że prawdopodobieństwo wylosowania czarnego klocka jest równe 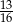 , prawdopodobieństwo wylosowania klocka w kształcie sześcianu jest równe
, prawdopodobieństwo wylosowania klocka w kształcie sześcianu jest równe  , a prawdopodobieństwo wylosowania klocka, który jest biały lub jest kulą jest równe
, a prawdopodobieństwo wylosowania klocka, który jest biały lub jest kulą jest równe 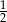 . Oblicz prawdopodobieństwo wybrania klocka, który jest białą kulą.
. Oblicz prawdopodobieństwo wybrania klocka, który jest białą kulą.
Pole trapezu równoramiennego opisanego na okręgu jest równe 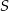 , a kąt ostry przy podstawie ma miarę
, a kąt ostry przy podstawie ma miarę  . Wykaż, że ramię tego trapezu ma długość
. Wykaż, że ramię tego trapezu ma długość 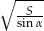 .
.
Dany jest nieskończony ciąg geometryczny 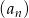 określony dla
określony dla 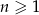 , w którym pierwszy wyraz jest liczbą naturalną, a iloczyn pierwszego i trzeciego wyrazu jest równy 1. Suma wszystkich wyrazów tego ciągu jest liczbą z przedziału
, w którym pierwszy wyraz jest liczbą naturalną, a iloczyn pierwszego i trzeciego wyrazu jest równy 1. Suma wszystkich wyrazów tego ciągu jest liczbą z przedziału 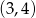 . Oblicz iloraz tego ciągu.
. Oblicz iloraz tego ciągu.
Punkty 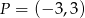 ,
, 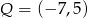 i
i 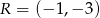 są środkami odpowiednio boków
są środkami odpowiednio boków 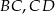 i
i 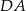 równoległoboku
równoległoboku 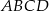 . Wyznacz współrzędne wierzchołków tego równoległoboku.
. Wyznacz współrzędne wierzchołków tego równoległoboku.
Wyznacz wszystkie wartości parametru  , dla których wykresy funkcji
, dla których wykresy funkcji 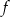 i
i 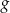 , określonych wzorami
, określonych wzorami 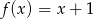 oraz
oraz 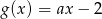 , przecinają się w punkcie o obu współrzędnych ujemnych.
, przecinają się w punkcie o obu współrzędnych ujemnych.
Wyznacz wszystkie wartości parametrów  i
i 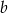 , dla których wykresy funkcji
, dla których wykresy funkcji
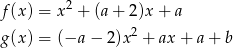
przecinają się w dwóch różnych punktach leżących na osi 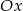 .
.
Podstawą ostrosłupa jest kwadrat 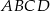 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych 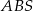 ,
, 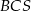 ,
, 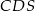 i
i 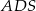 są odpowiednio równe: 740,
są odpowiednio równe: 740, 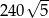 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa.
Rozpatrujemy wszystkie graniastosłupy prawidłowe czworokątne, których pole powierzchni całkowitej jest równe 2. Oblicz długości krawędzi tego graniastosłupa, który ma największą objętość. Podaj tę największą objętość.

