/Szkoła średnia
Egzamin Maturalny
z Matematyki poziom rozszerzony 9 maja 2017 Czas pracy: 180 minut
Zadania zamknięte
Liczba 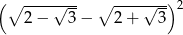 jest równa
jest równa
A) 2 B) 4 C) 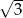 D)
D) 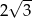
Nieskończony ciąg liczbowy jest określony wzorem 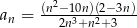 dla
dla 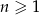 . Wtedy
. Wtedy
A) 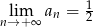 B)
B) 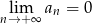 C)
C) 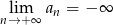 D)
D) 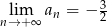
Odcinek 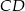 jest wysokością trójkąta
jest wysokością trójkąta 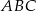 , w którym
, w którym 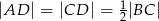 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 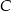 i promieniu
i promieniu 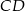 jest styczny do prostej
jest styczny do prostej 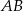 . Okrąg ten przecina boki
. Okrąg ten przecina boki 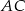 i
i 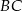 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 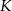 i
i 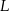 .
.
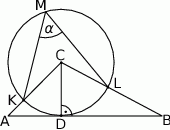
Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 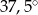 B)
B) 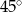 C)
C) 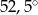 D)
D) 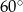
Dane są punkt 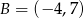 i wektor
i wektor ![→ u = [−3 ,5]](https://img.zadania.info/zes/0087868/HzesT26x.gif) . Punkt
. Punkt 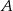 , taki, że
, taki, że 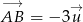 , ma współrzędne
, ma współrzędne
A) 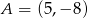 B)
B) 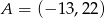 C)
C) 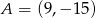 D)
D) 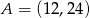
Zadania otwarte
Reszta z dzielenia wielomianu 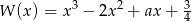 przez dwumian
przez dwumian 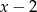 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Funkcja 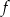 jest określona wzorem
jest określona wzorem 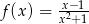 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 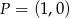 .
.
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 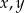 prawdziwa jest nierówność
prawdziwa jest nierówność
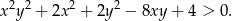
W trójkącie ostrokątnym 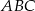 bok
bok 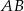 ma długość
ma długość  , długość boku
, długość boku 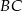 jest równa
jest równa  oraz
oraz 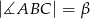 . Dwusieczna kąta
. Dwusieczna kąta 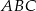 przecina bok
przecina bok 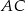 trójkąta w punkcie
trójkąta w punkcie 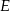 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 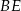 jest równa
jest równa 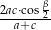 .
.
W czworościanie, którego wszystkie krawędzie mają taką samą długość 6, umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna 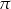 , równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej
, równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej 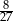 objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka
objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka 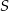 kuli od płaszczyzny
kuli od płaszczyzny 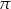 , tj. długość najkrótszego spośród odcinków
, tj. długość najkrótszego spośród odcinków 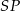 , gdzie
, gdzie 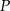 jest punktem płaszczyzny
jest punktem płaszczyzny 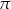 .
.
Rozwiąż równanie 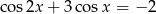 w przedziale
w przedziale 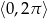 .
.
W pudełku znajduje się 8 piłeczek oznaczonych kolejnymi liczbami naturalnymi od 1 do 8. Losujemy jedną piłeczkę, zapisujemy liczbę na niej występującą, a następnie zwracamy piłeczkę do urny. Tę procedurę wykonujemy jeszcze dwa razy i tym samym otrzymujemy zapisane trzy liczby. Oblicz prawdopodobieństwo wylosowania takich piłeczek, że iloczyn trzech zapisanych liczb jest podzielny przez 4. Wynik podaj w postaci ułamka zwykłego.
Wyznacz wszystkie wartości parametru 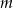 , dla których równanie
, dla których równanie
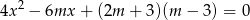
ma dwa różne rozwiązania rzeczywiste 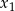 i
i 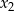 , przy czym
, przy czym 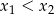 , spełniające warunek
, spełniające warunek
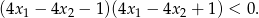
Wyznacz równanie okręgu przechodzącego przez punkty 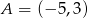 i
i 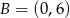 , którego środek leży na prostej o równaniu
, którego środek leży na prostej o równaniu 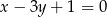 .
.
Liczby 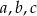 są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa 27. Ciąg
są – odpowiednio – pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa 27. Ciąg 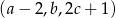 jest geometryczny. Wyznacz liczby
jest geometryczny. Wyznacz liczby 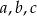 .
.
Rozpatrujemy wszystkie walce o danym polu powierzchni całkowitej 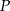 . Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz tę największą objętość.
. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz tę największą objętość.

